FOC与SVPWM学习2

1. FOC两个重要变换及其意义

   1. 两个变换——clark变换和park变换
   2. 三相电（三坐标轴，时变）–clark变换–>(α, β)正交坐标系的二维矢量（两轴，时变）
      首先由于三相系统由三个幅值相等、频率相同、相位差为120°的正弦交流电组成，对于三相瞬时电流有约束：I_a + I_b + I_c = 0
      （所以实际我们最少只需要进行两相电流采样即可直到三相
      电流.）
      将三相电流通过矢量加法合成为定子电流矢量，其中α是空间向量算子，用于将复平面上矢量(I_b,0)或(I_c,0)旋转为代表b相或c相电流的空间矢量，α = e^j*2/3π
      
      
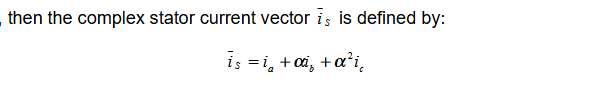
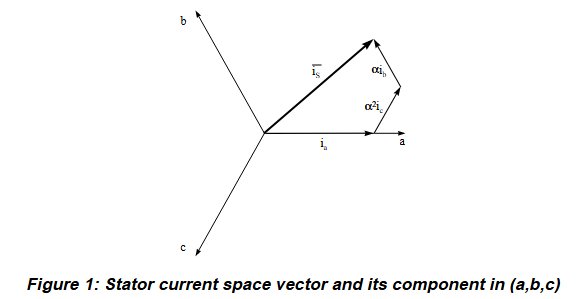
      得到i_S后, 在(α,β)坐标系中将其分解为i_Sα和i_Sβ, 即完成了clark变换
      
      
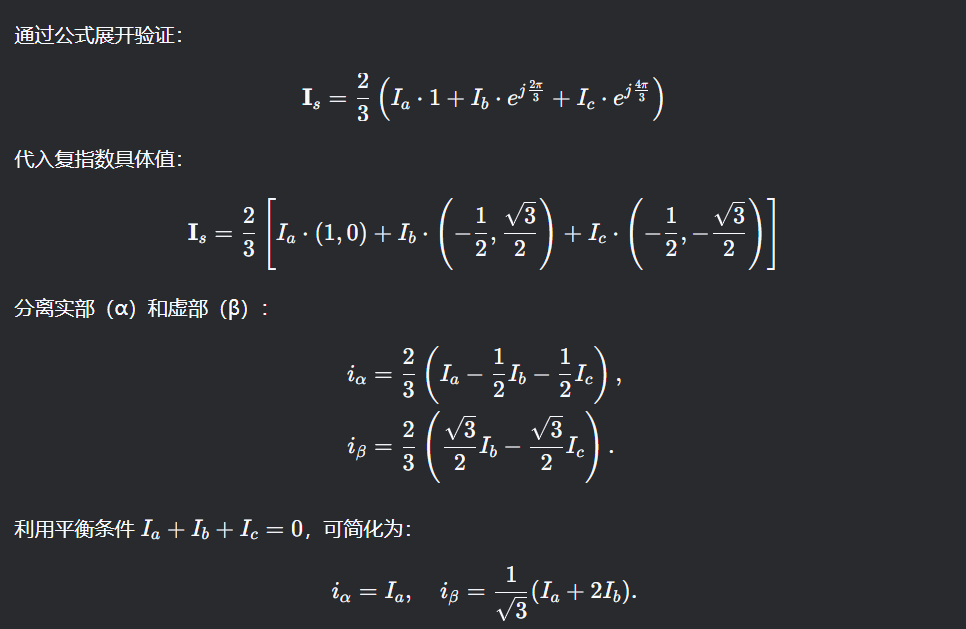
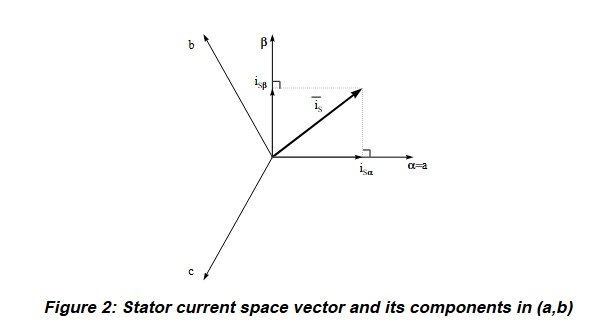
   3. (α, β)正交坐标系的二维矢量（两轴，时变）–park变换–>(q, d)坐标系上的二维矢量（两轴，时不变）
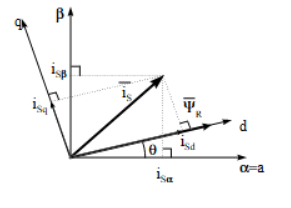
      首先我们需要知道电机磁链的角度, 即电角度θ. park变换是要将当前电流矢量投影到一个跟随电机磁链旋转变化的坐标系(d, q), 其中d轴对准磁链方向. 投影后d轴电流直接影响磁场强度, q轴电流直接控制转矩, 这样就实现了励磁电流和转矩电流的解耦.
      数学推导: 此处假设电角度θ已知(通过编码器或三相反电动势反推获得)
      
      
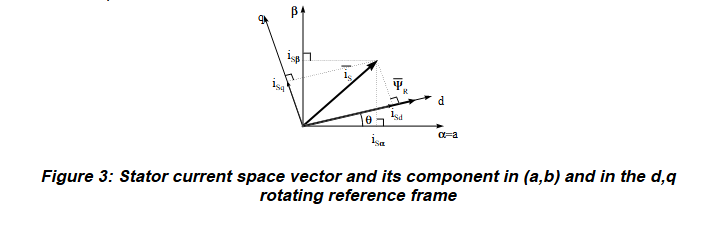
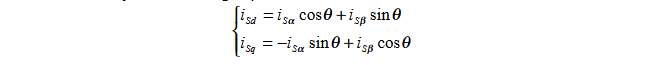
      由此我们就可以计算出此时的励磁电流和转矩电流
      进一步理解: park变换的特殊性在于引入了电角度θ, 虽然我们说dq轴上的电流是和时间无关的, 但是实际上实际应用中θ是时变的. FOC最大的好处是可以实现直接转矩控制, 即能在不用考虑时间变化的因素下, 直接给出一个对转矩的需求并且轻松的到所需的转矩电流. 至于如何真正实现控制, 那就需要反变换了, 也就是接下来要讲述的内容.
   4. 以上便是已知三相电流和电角度, 如何求得励磁电流和转矩电流, 并能计算转矩的过程(前文已经提到, 对于SPMSM, 转矩与转矩电流成严格正比关系)

2. park变换与clark变换的逆变换——给出所需的dq轴电流并反推出三相电流（下文再说吧，学不动了orz