之前学信号与系统的适合对于傅里叶变换只是一知半解,仅仅知道它能实现时域和频域之间的转换。今天学习自动控制原理的时候,课程里的哥们给我复习了傅里叶变换基础,但是他讲了自己的理解,我觉得对我来说这种理解很新奇很有意思,更重要的是很具象。
视频链接:【【中英字幕】Brian Douglas Control Theroy | 自动控制原理】 【精准空降到 01:24】 https://www.bilibili.com/video/BV1WT4y1M7rm/?p=7&share_source=copy_web&vd_source=44cc7f69ddf80fe5bcd5d6df9537b058&t=84
视频分上下两集, 第一集主要讲傅里叶变换但有点小错误, 第二集对错误进行修正, 以及讲了傅里叶逆变换.
首先观察傅里叶变换公式如下:
如Brian老哥所说,我们应该把后面的复指数看作是一堆正弦函数.
事实上也确实如此,因为欧拉公式: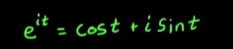
我们知道, 傅里叶变换是将信号的频谱提取出来, 好比寻找一个信号中有多少成分的某个频率的正弦函数. 在这里老哥举了一个例子:
15块钱里, 有多少个五块钱? 答案是3.
那么类比到傅里叶变换中, 同样的问题可以提出为: 在信号x(t)中, 有多少成分的15Hz正弦信号?
我们计算钱的问题的时候, 本质上是在做除法, 15/5 = 3.
我们为了解决信号的问题而使用傅里叶变换, 实际上也是在做除法. 抽象的说, 我用一个特定频率的正弦信号去除x(t), 就可以知道x(t)中有多少这个频率的信号了, 这其实完全是在时域上完成的操作.
接下来通过数学和图像来证明我们的类比是否正确.
- 首先, 关于时域上的除法, 基本无需证明, 因为傅里叶变换积分符号内的内容是
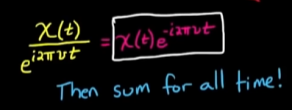
*其实就是用x(t)除以一个正弦信号, 只是它变成了复指数信号, 我们一眼看不出来; *而且复指数信号里面有实部的cos成分来提取这个频率在x(t)中的幅度, 还有虚部的sin成分来提取这个频率在x(t)中的相位. 所以我们就能提取到所有的信息.
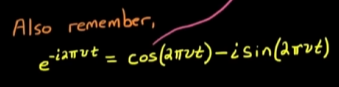
- 其次, 当我们加上积分符号, 就意味着用所有频率范围对x(t)做一次检测, 提取出其包含的频率范围并相加, 最后我们就能得到频谱, 这是符合逻辑的.
- 据具体的例子:
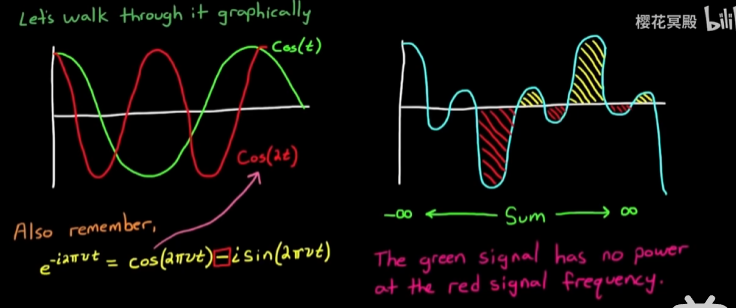
例一, 当x(t) = cos(t)时, 用cos(2t)去检测(相乘), 得到的是一个在无限时间内相加为0的函数, 也就是说cos(t)在 f = 派 的频率上没有功率; 如果用cos(t)去检测, cos(t)*cos(t)当然会得到一个直流分量和高频分量, 无限时间下相加就不为零(甚至是无限), 也就是说cos(t)在 f = 2*派 上是有功率的.
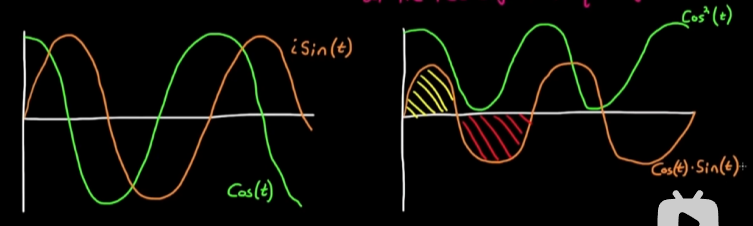
例二, 当我们考虑相位, 同样是x(t) = cos(t), 用 cos(t) + isin(t) 去检验, 会在实部上得到一个无穷大的值, 虚部上得到一个零值, 也就是直观地说x(t)在 f = 2*派 上有功率, 且相位为0; 同理我们考察x(t) = sin(t), 实部为0而虚部为无穷, 则x(t)在 f = 2*派 上有功率, 且相位为90°. 功率的计算对应于复平面上向量的模长, 也就是 根号下(实部² + 虚部²); 同理对于x(t) = cos(t + 45°), 我们能得到的实部和虚部大小相等. - 上述例子中, 从积分符号出来以后的值都是无穷, 如何衡量实际成分大小? 冲激函数δ(v)就是一个很好用的工具, 因为在频域上进行平移即可表示不同频率, 乘以某个系数就可以表示这个频率的成分大小, 而不丢失”积分结果为无穷大”的信息. 例如cos(t)的傅里叶变换就为:
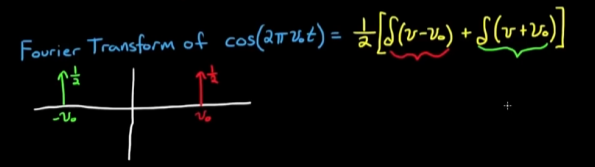
- 虽然说表述上, 是用一个信号”除”另一个信号, 但是实际上还是乘法, 因为复指数信号指数部分加一个负号, 也就是正弦信号变变符号而已. 说到用乘法来提取信息, 就让我想到这学期学习的相干解调法, 就是通过调制信号乘以本地同频同相载波, 来提取信息的. 那么我们可不可以说, 相干解调其实也是用”信号除以频率成分”来提取信息的呢?
于是brian对傅里叶变换总结如下: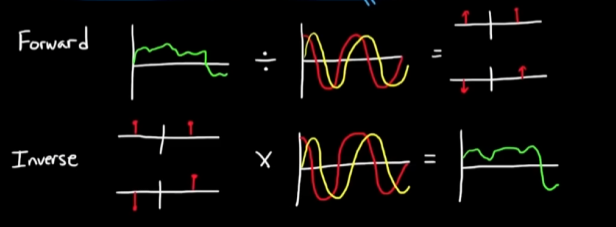
正变换: 通过”除法”进行频率提取, 将所有频率的信息加起来就得到了频谱
逆变换: 我们有频谱, 根据频谱上各个分量的信息加起来, 就还原了信号
