Bode图1

1. bode图——可视化整个频谱中系统的频率响应

2. 我们为什么要研究LTI system/为什么要尽量将一个系统设计成LTI system?：

   1. LTI系统的运算是有限的, 加减乘除, 微分积分
   2. LTI系统输入一个正弦信号, 输出还是正弦信号且频率不变, 只有幅度和相位改变; 由于我们可以将任意信号分解为正弦信号的组合, 也就是在频域上表示, 所以LTI系统的这个特性非常适合频域上的分析.

3. LTI对单一频率的响应可以直接通过计算得到, 但是想了解系统对整个频谱的响应, 就需要用到bode图进行直观描述

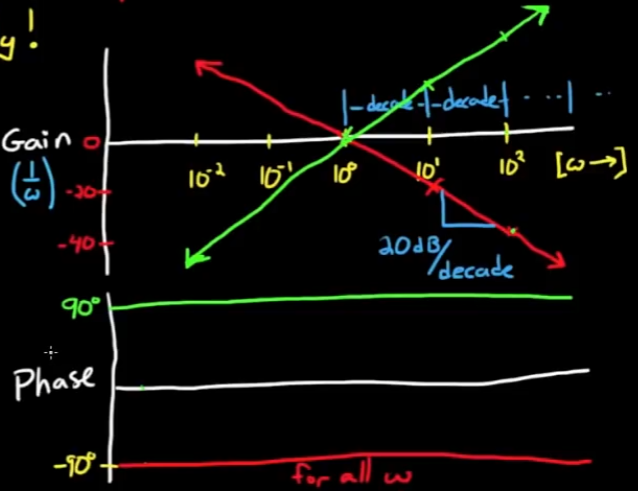
4. bode图由两部分组成, 横轴都是输入信号的频率, 向上的纵轴是系统对输入信号的响应增益, 向下的纵轴是系统对输入信号的相移. 其中增益用分贝dB来表示, dB计算方法为:
   
   其中A是输出信号振幅, A0是输入信号振幅
   一般来说, 分贝计算前面的系数是10, 而正弦信号功率是与振幅平方成正比的, 所以平方提到对数符号前面就成了2倍.

5. bode图是对系统频响的直观刻画, 那么系统传递函数就是准确的数学表达.

   1. 对系统进行Laplace变换, 得到输入输出比值, 等号右边即是传递函数.
   2. 由于我们要研究的是系统的稳态响应, 所以选择s = σ + jω中σ = 0的时候
      a. 因为e^(σ + jω)中, jω是稳定的正弦信号, 而σ描述的是信号的衰减, 所以σ代表的是变化而不是稳定
      b. σ = 0时Laplace变换相当于Fourier变换, Fourier变换则是专门研究信号稳态成分的分析
   3. 
   4. 传递函数的实部和虚部可以直接刻画系统增益和相位
      
      如图, 将实部和虚部画在虚平面上, 从零点发出相位指向那个点为一个向量, 向量长度即是增益, 向量与实轴夹角即是相位.
      频率变化的时候, 虚平面上向量改变, 即可直观得知系统对整个频谱的响应.