对于一个系统, 我们经常会关心它的响应在时间趋于无穷的时候是什么样的, 也就是系统趋于稳定的时候的值是多少(当然也会有系统无法趋于稳定, 那也就不可能得到这个值, 这种系统不在讨论范围之内).
系统建模后在时域上的函数表达很可能是一个微分方程, 如果是二阶或者更高阶的方程, 对它求时间上的极限可能就有一些难度. 我们只关心时间趋于无穷的情况, 而不过问整个过程, 所以不应该在时域上死磕. 频域上有一个很好的方法可以帮助我们直接得到”终值”而无需解微分方程, 那就是终值定理.
终值定理的直接数学表达如下:
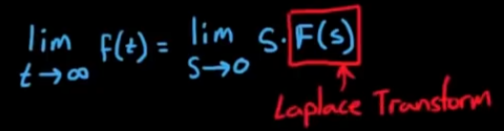
好像很简单, 但是终值定理有其适用范围, 不是所有传递函数都适用.终值定理适用范围
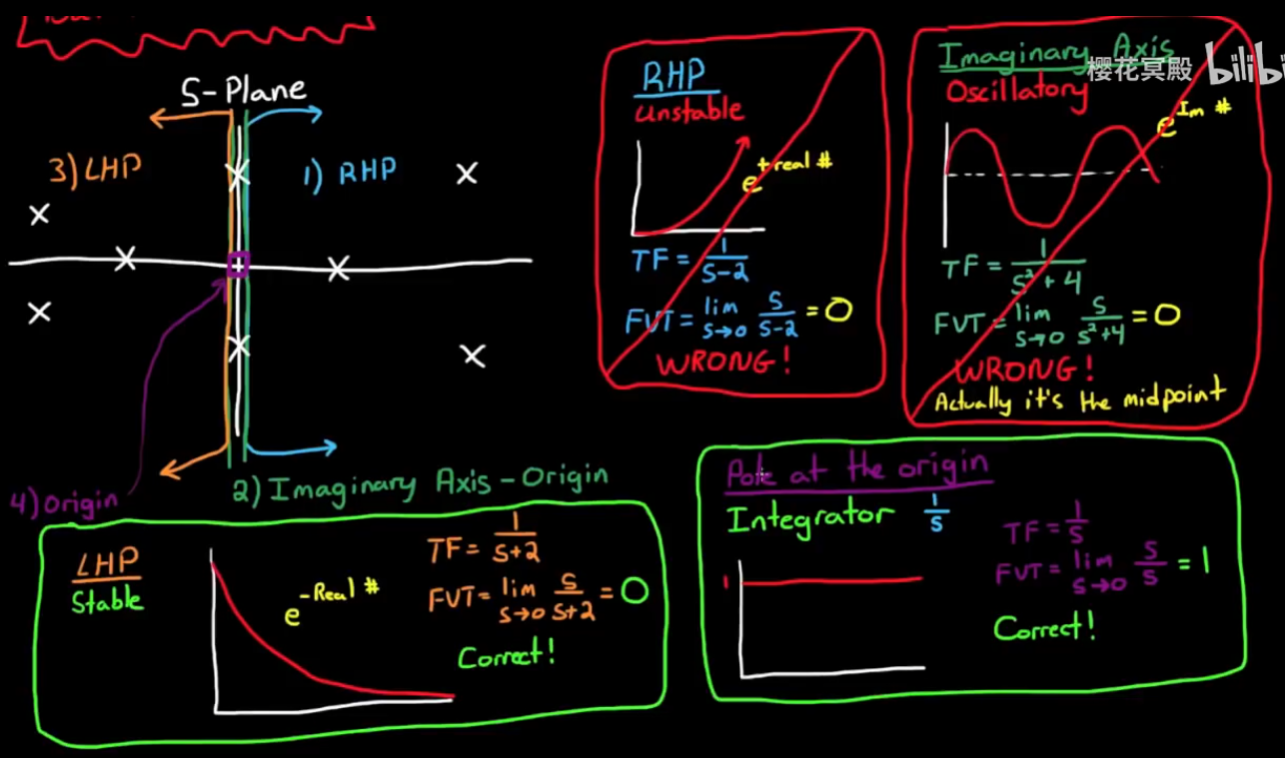
将s平面分为四个区域: 左半, 虚轴, 原点, 右半, 互不交叉, 则终值定理仅适用于极点在左半区和原点的传递函数, 原因如下:
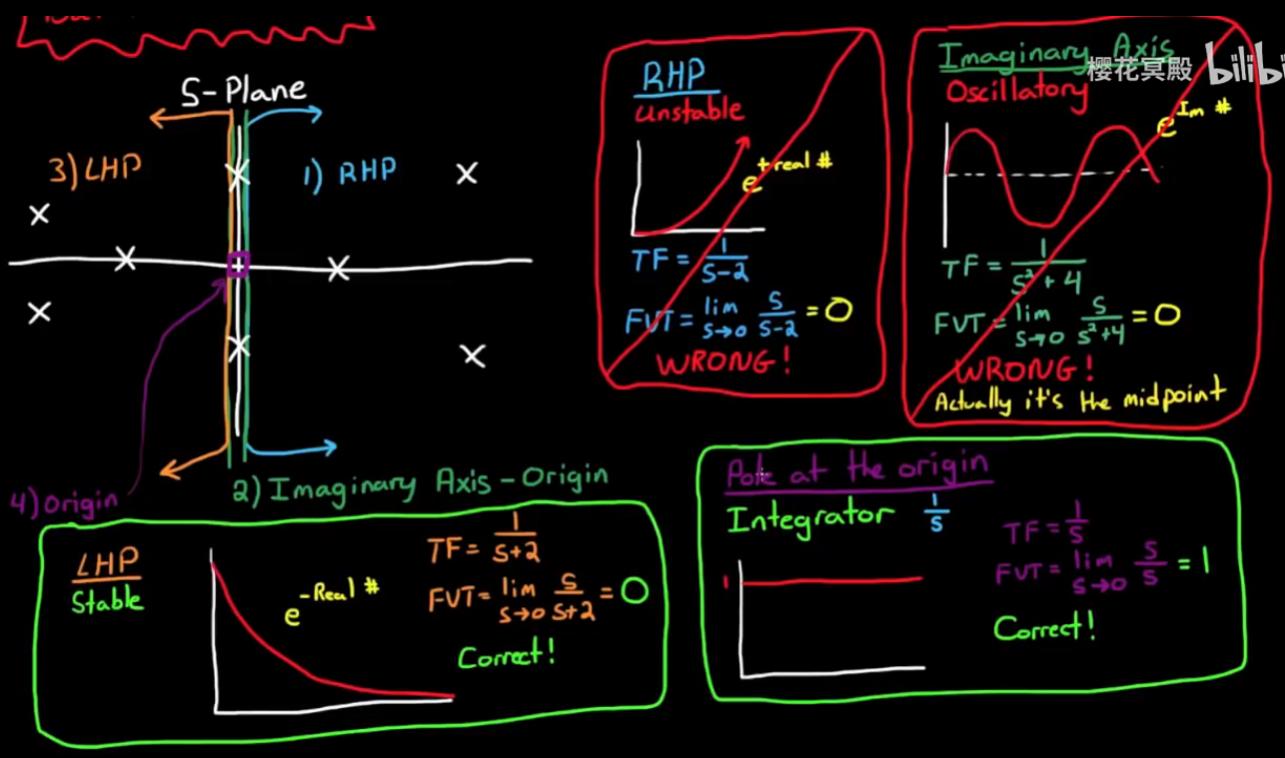
- 当一个传递函数有极点在右半边, 那意味着它有指数增长的分量, 进一步意味着它在时间趋于无穷的时候取值为无穷, 而对它使用终值定理会得到错误的结果.
- 当极点在虚轴上, 这意味着传递函数有振荡的分量而没有衰减分量, 进一步意味着它的终值是不确定的, 对它使用终值定理会得到振荡的均值, 也就是0, 也是不正确的.
- 当极点处在左半区时, 传递函数存在指数衰减的分量, 最终会趋于0, 此时可以使用终值定理.
- 当极点处在原点时, 它是一个积分器, 积分器的脉冲响应是一个定值, 此时也可以使用终值定理
接下来讨论的所有传递函数都默认是可以使用终值定理的函数, 也就是极点在原点或左半区.
传递函数类型: 按原点处的极点数来分类
不知道为啥这么分, 但是确实是可以分类的:- 原点处有0个极点: Type 0
原点处没有极点, 则极点在左半区, 频率响应为指数衰减, 终值趋于0; - 原点处有1个极点: Type 1
原点处有一个极点, 也就是积分器, 频率响应为常数值, 终值趋于常数值; - 原点处有2个极点: Type 2
原点处有两个极点, 二重积分作用下, 终值趋于无穷; - 以此类推, 更多极点对应更多Type, 终值都是无穷.
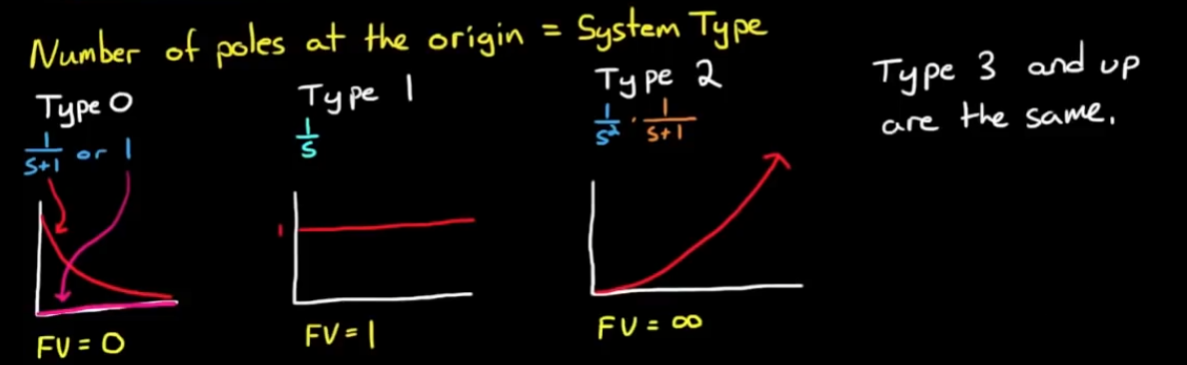
总结: 极点在左半区, 不在原点上时, 无论几个极点, 终值都是0; 原点有一个极点, 终值为常数值, 原点有两个及以上极点, 终值为无穷.
- 原点处有0个极点: Type 0
利用终值定理求传递函数的脉冲响应终值
例如:
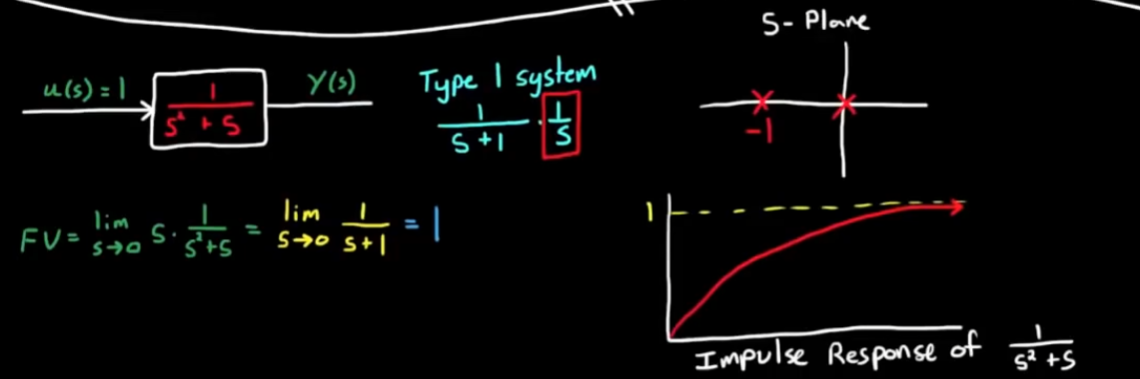
step1, 找出极点, 判断是否可用终值定理
step2, 计算
非常简单
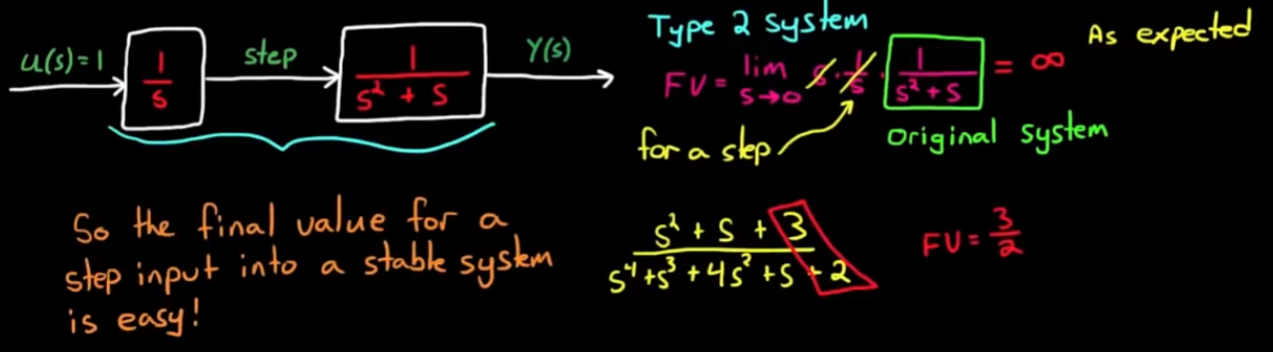
但是如果我们想求阶跃响应的终值呢?利用终值定理求传递函数的阶跃响应终值
阶跃是对脉冲的积分, 所以我们可以将一个积分器和传递函数组合, 仍然输入脉冲, 即可得到阶跃响应.
注意到, 我们使用终值定理实际上是给传递函数在原点处增加一个零点, 而添加积分器, 则是给传递函数在原点处添加一个极点. 零点与极点相互抵消, 事实上系统阶跃响应的终值就是将传递函数的所有s取极限, 如下图的数学推导:
终值定理在负反馈系统中的应用
终于来到了应用部分, 知道一个传递函数的响应的终值有什么用? 对于一个负反馈控制系统, 我们希望误差尽可能小或不发散, 此时如果我们用终值定理求误差在不同输入(脉冲, 阶跃, 斜坡, 加速度, and so on)下的终值, 我们就可以用此指导系统的设计.
一般来说负反馈系统的输出并不是误差, 所以需要重写传递函数:
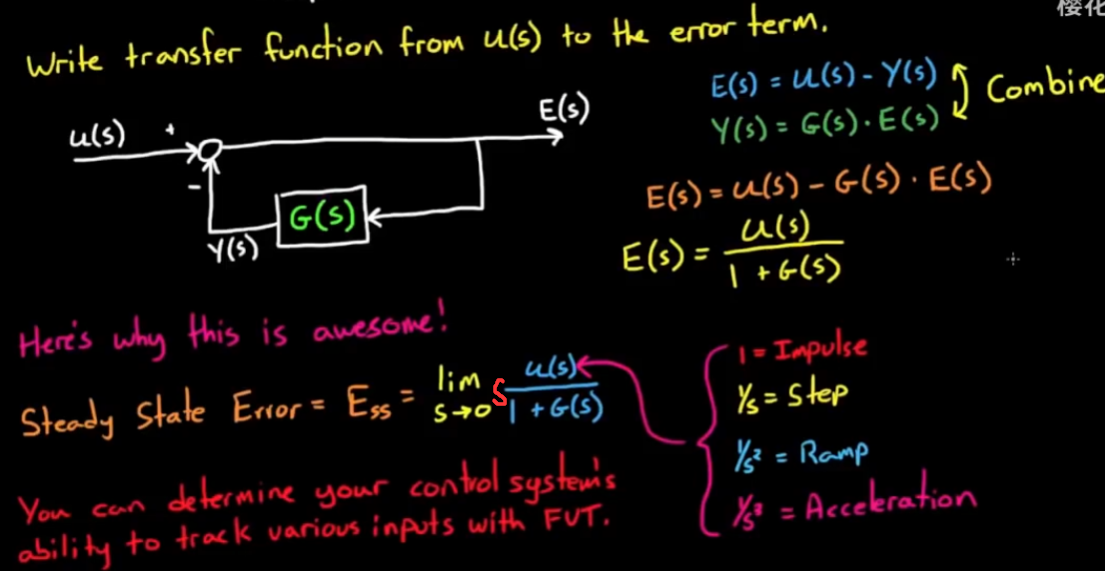
当我们通过框图求出输入到误差的传递函数, 就可以对它使用终值定理, 并且将u(s)替换为不同的输入, 看看系统的终值如何, 是趋于0, 趋于常数, 还是发散? 这有助于我们设计一个符合要求的系统.
例如针对特定输入, 终值很小或趋于0, 此时我们可以判定我们对G(s)的设计是充分的, 否则需要考虑重新设计.
“一个设计良好的控制系统是这样设计的: 输出尽可能地跟随输入“. 在输入极点增加时(例如从输入脉冲变为输入阶跃), 系统的类型在增加, 此时若输出还能跟随输入, 那么在这个输入下的系统设计的就是良好的. 虽然再增加输入极点, 输出终值可能就无法收敛, 但是, 满足需求即可.
如果有跟随更多极点输入的需要, 就需要往系统设计中加入在原点处的零点.
“this is how we design our systems.“