观前提醒: 本文存在大量不加证明的结论, 想知道原理的, 去看youtube上Brian的这一期视频,底下会有相关视频链接.
劳斯判据: 避免求解高阶多项式的根而直接得出系统的稳定性
- 首先需要明确的是, 一个稳定的系统不可能存在虚平面右半区的极点, 因为一旦存在这样的极点, 终值必定为无穷大.
- 不加证明地给出以下判据: 多项式的所有根都在左半平面上, 当且仅当, 其系数的一组代数组合具有相同的符号.
- 很好理解, 例如所有符号除了某一个符号以外都是+, 那么意味着特征方程因式分解时, 必定存在(s-a)的项, a>0, 即有右半平面的根, 系统必定不稳定.
- 这并不是说看到所有系数符号相同就可以判定系统具有稳定性, 而是当所有系数符号不是都相同时, 可以断言系统不是稳定的. 例如:
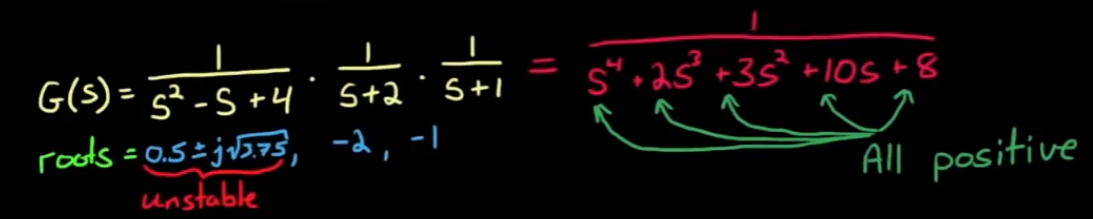
- 如何能断定系统是稳定的? 结合劳斯数组进行判断.
劳斯数组: 规则+系数 = 稳定性判断, 劳斯数组的填充方法.
- 劳斯数组是一个列表, 通过按照某些规则填入多项式系数并且做一些计算, 可以直接得到系统稳定性/右半区极点数量. 列表的行列数量由多项式最高次幂决定, 下面会提及.
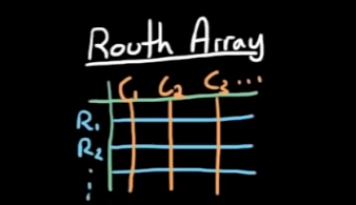
- step1, 将多项式写成降幂形式
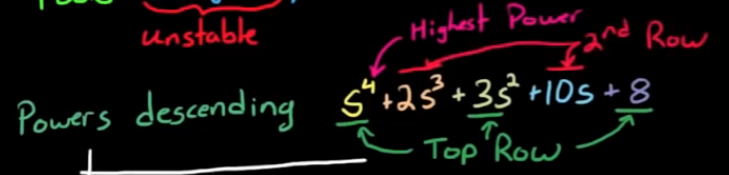
- step2, 将降幂的系数按照波浪形式写入第一行的第二行, 没有系数的项默认系数为0.
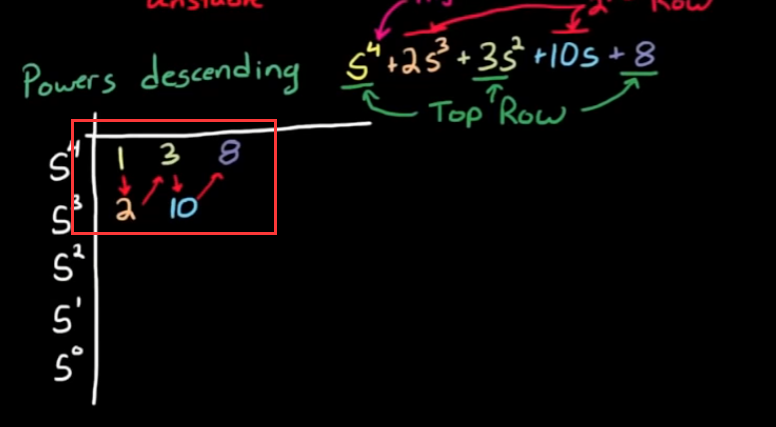
- step3, 仍然是不加证明地给出以下操作规则, 以图形化形式较为直观:
- 第一个数字计算方法如上, 想象一个8字, 从左下角B开始, 走到右上角C代表B*C, 从C走到左上角A再走到右下角D代表 B*C - A*D, 最后走回左下角B代表(B*C - A*D) / B.
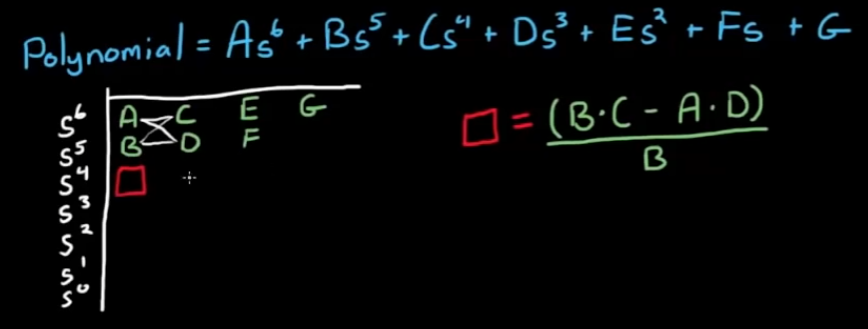
- 第二个数字是将8字拉长, 起点仍然从第一列开始, 计算方法同理, (B*E - A*F) / B.
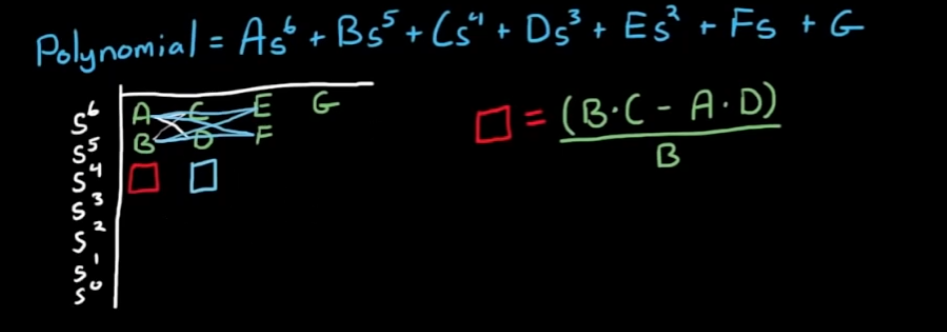
- 计算第三个数字同前, 注意留空的地方要补0.
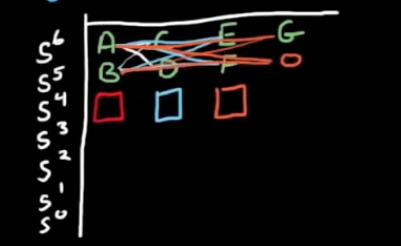
- 计算到列尾的时候, 不再向后计算而是换行. 换行后以刚刚计算的列为基础计算新的列, 直到列尾, 计算方法同前.
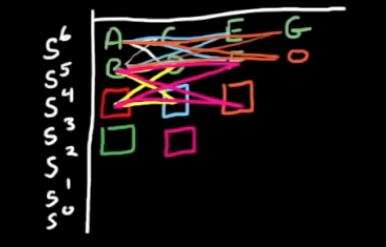
- 一旦算到最后, 就可以用第一列的系数符号来判断系统在右半区有几个极点, 这里用一个实际的例子说明:
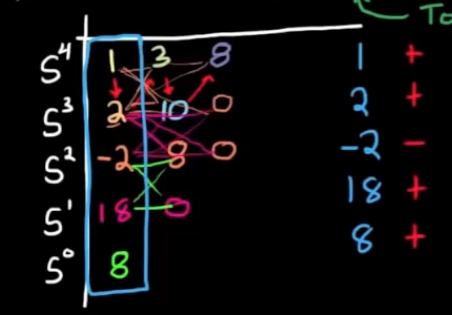
- 第一个数字计算方法如上, 想象一个8字, 从左下角B开始, 走到右上角C代表B*C, 从C走到左上角A再走到右下角D代表 B*C - A*D, 最后走回左下角B代表(B*C - A*D) / B.
- step4, 如上图, 计算完成后观察到第一列有两次符号变化, (+)=>(-)=>(+), 则说明右半区存在两个极点, 系统是不稳定的. 这与直接计算结果一致:
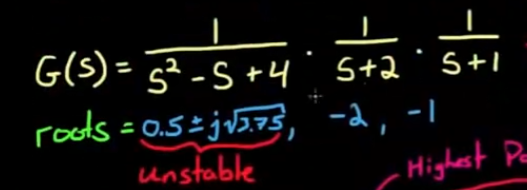
劳斯判据的两种特殊情况
当劳斯数组中某一行存在0, 同一行的后面至少有一个非零项.
- 例子如下, 当出现这种情况时, 一定存在右半区的极点, 因为这种情况必然会出现计算为负数的情况:
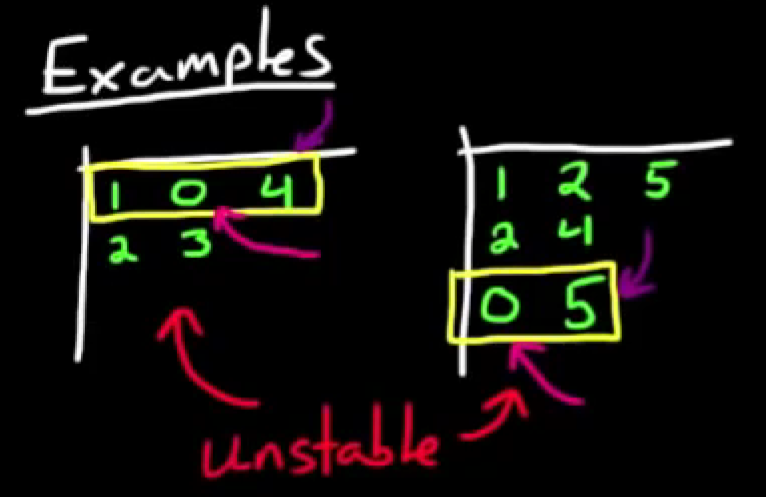
发现数组中填入数字为这种情况, 则可以立刻断言系统不稳定并可以不继续计算. - 当对右半区究竟有几个极点感兴趣, 可以继续计算, 但是要将0设置为ε(变量, 代表任意小的数字), 按照规则计算之后, 再将ε->+0, 得到+∞看作正数, -∞看作负数, 符号变化次数仍然代表右半区极点数量.
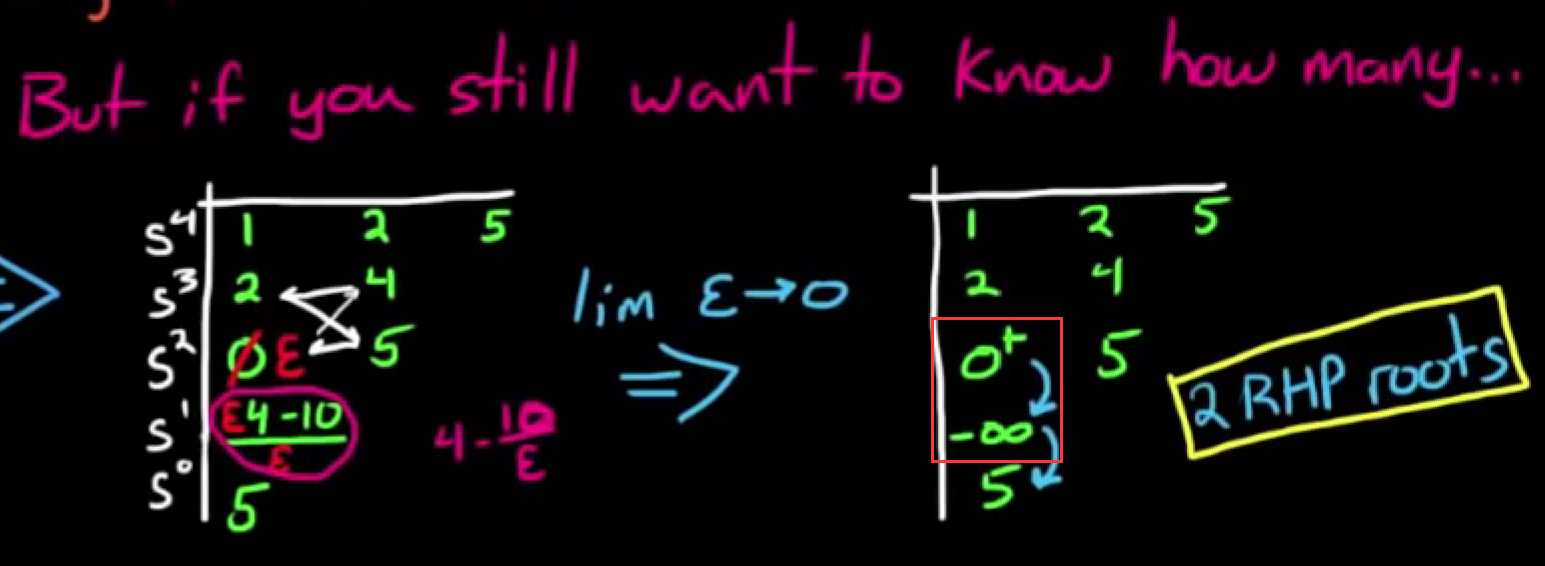
- 更多的例子:
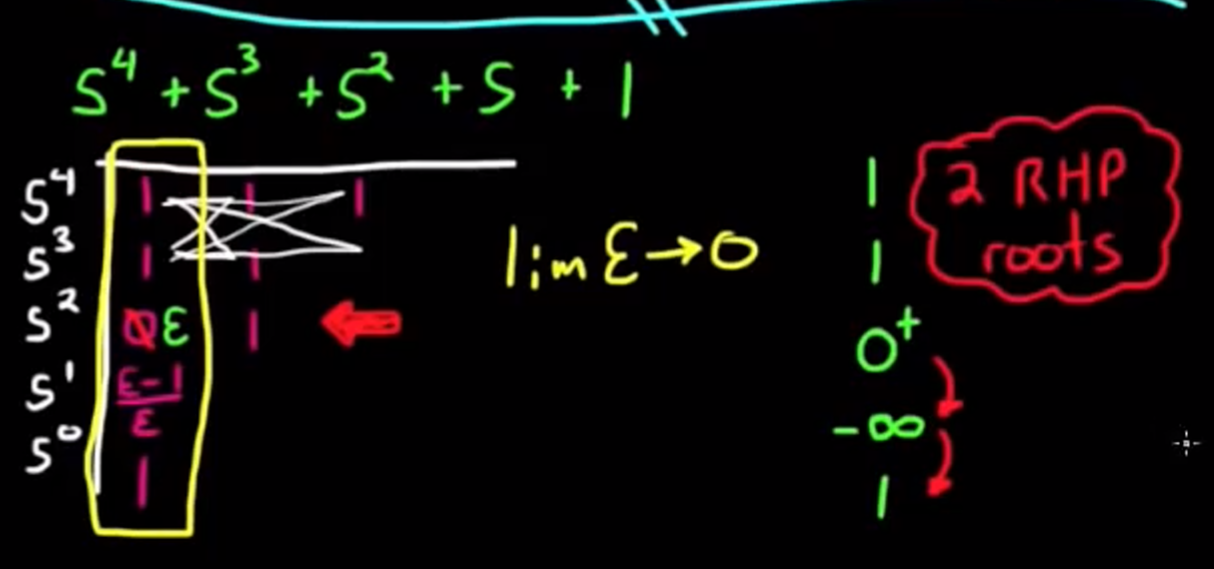
- 例子如下, 当出现这种情况时, 一定存在右半区的极点, 因为这种情况必然会出现计算为负数的情况:
当劳斯数组中某一行全为0时,
- 特征方程的根只可能存在以下情况:
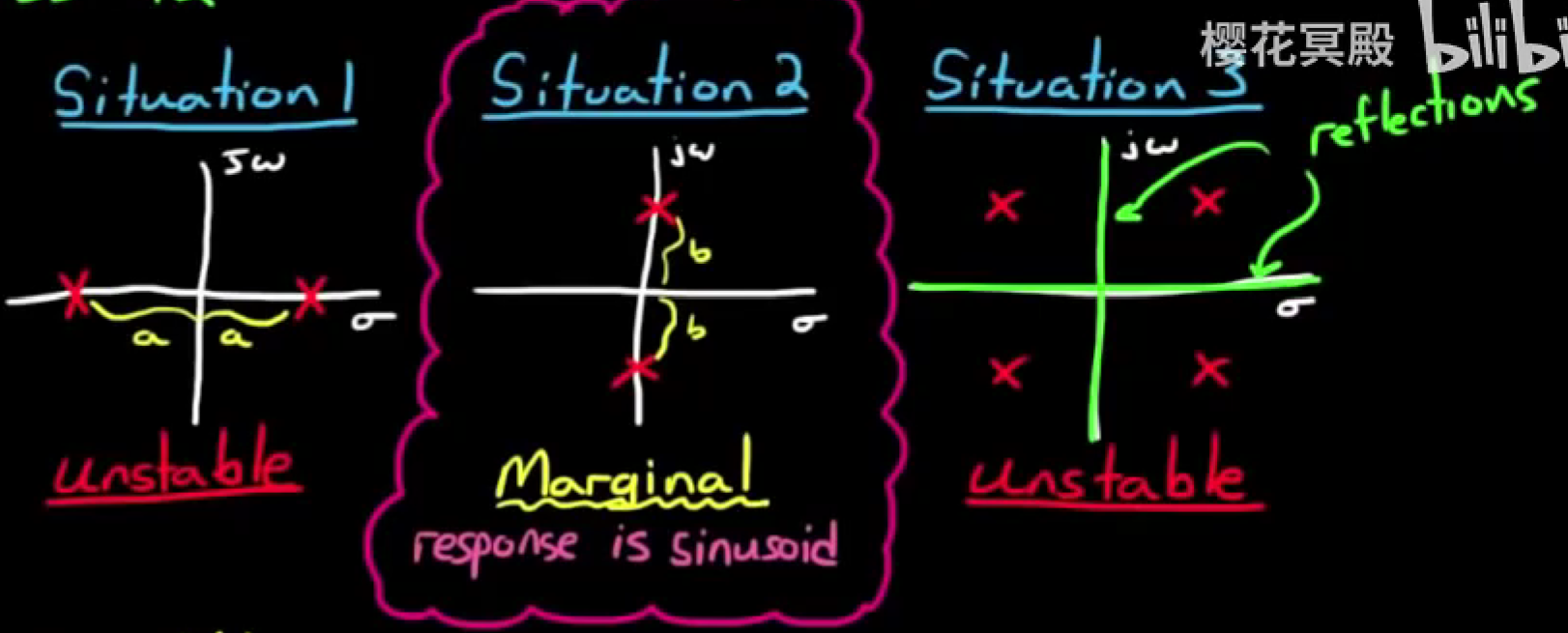
情况1: 关于jw轴对称的实根
情况2: 关于实轴对称的纯虚数根
情况3. 关于jw轴和实轴对称的两对复数根
情况1, 3都是指向不稳定的系统, 而情况2的系统处于临界稳定状态.(Brian的视频是这么说, 响应是正弦的, 但是正弦的响应真的能说是”稳定的”吗?) - 要判断具体属于哪种情况, 需要搞一堆很复杂的运算, 但是实际上我也没看懂, 特别是如何写辅助多项式那一部分, 我尽量讲讲过程, 如下:
step1, 选择全0行的上一行, 作为辅助多项式的系数来源.
step2, 构造辅助多项式, 规则: 选取的行是哪个次幂, 就从这个次幂开始降幂, 间隔选取幂次作为辅助多项式的幂次, 例如从六次开始, 就选取六次, 四次, 二次, 零次(通过Brian视频和wikipedia的描述推断得到的规律, 不一定准确, 需要进一步验证). 例如:

以及
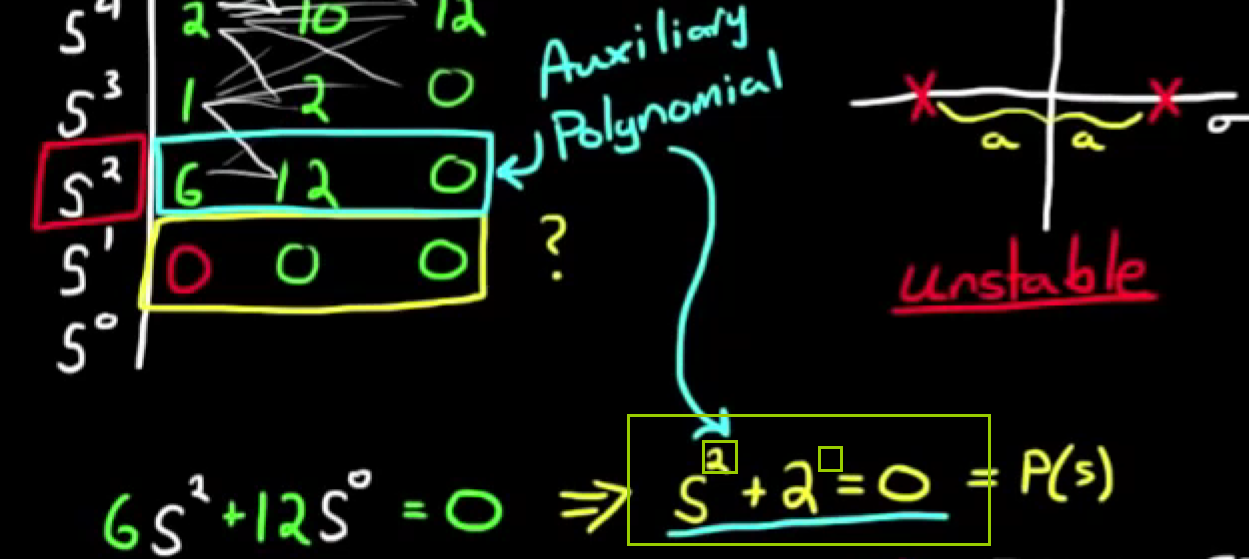
step3, 对辅助多项式P(s)求导, 用得到的系数替换全零行, 继续填写劳斯数组. 最后得到完整的劳斯数组再来判断, 若右半区没有根, 则说明系统是临界稳定的, 属于上述出现全零行的第二种情况. - 对于这种特殊情况, 有一个有趣的特性, 就是当且仅当只有一行全0, 则辅助多项式存在, 且是原特征方程的一个因式, 即作多项式除法没有余数.
- 并且对于因式分解后的Q(s) = P(s) * R(s), P(s)和R(s)可被看作两个独立的特征方程, 而在劳斯数组中, 辅助多项式系数对应的那一行之上的部分, 对应R(s)的根的情况, 反之那一行之下的部分, 对应辅助多项式的根的情况, 说的有点绕, 直接上图:

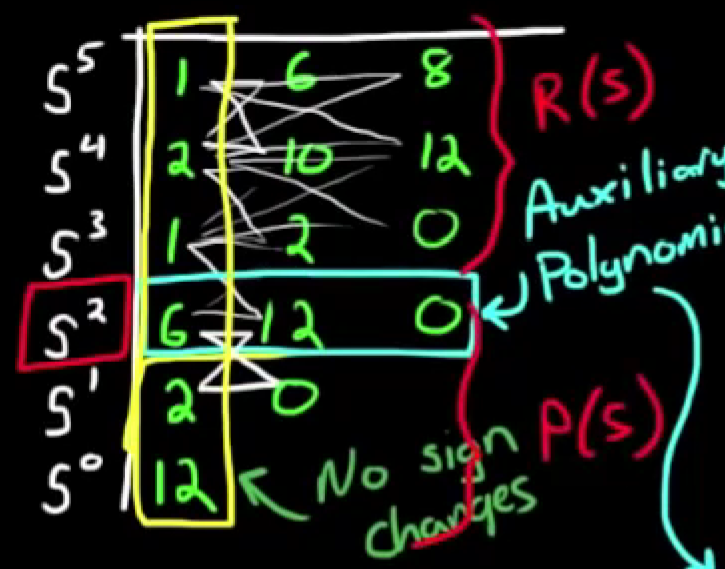
- 特征方程的根只可能存在以下情况:
劳斯判据的应用
当特征方程十分复杂, 无法直接方便求解出零极点时, 可以使用劳斯判据来判断系统稳定性, 并且通过一些计算, 可以求得系统的稳定裕度 (在保持稳定的前提下, 最大能增加多少增益?)
典型的闭环控制系统框图如下: 一个稳定的开环控制系统被加上了反馈回路, 并且被加上k倍的增益, 来保证得到响应足够快(足够大), 而不至于使系统变得不稳定. 由于这个系统十分复杂, 我们不好直接解出零极点, 所以带上变量k填充劳斯数组, 就可以有效得到使系统保持稳定的增益范围.
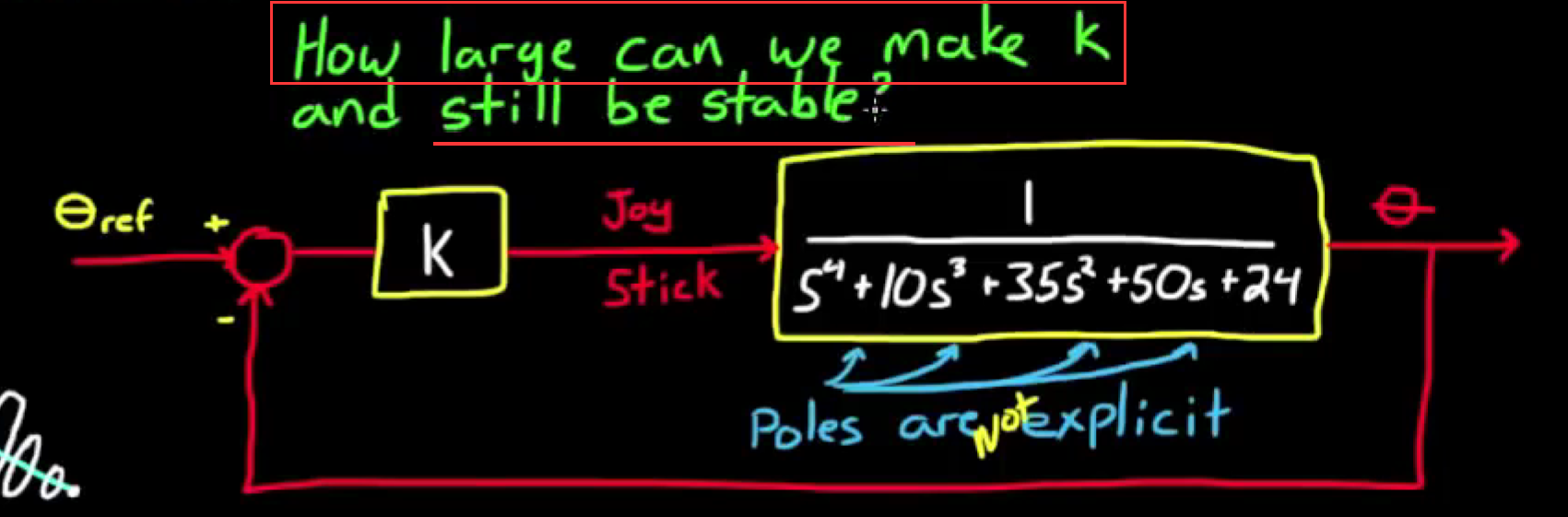
以下是步骤:
- step1, 考虑整个闭环控制系统, 系统重写系统传递函数为如下, 得到新的特征函数
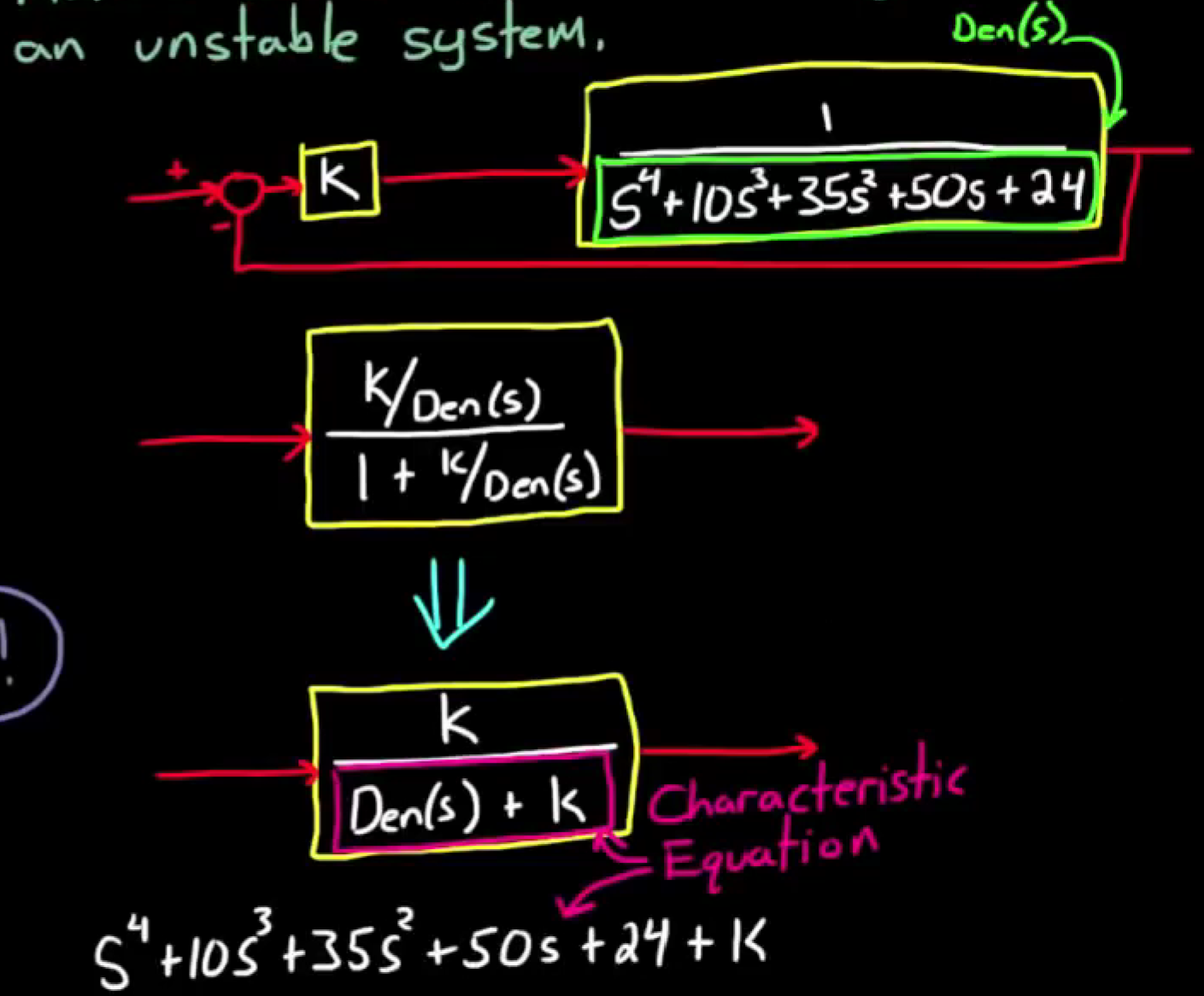
- step2, 用新的特征函数填写劳斯数组, 保持k为一个变量, 如下图左侧部分:

- step3, 为了保持系统稳定, 第一列符号不能变, 于是我们得到了关于k的不等式, 对多个不等式的解求交集, 我们就得到了使控制系统保持稳定的k的范围, 如上图右侧部分. 于是系统的稳定裕度表现为 k<126.
- step1, 考虑整个闭环控制系统, 系统重写系统传递函数为如下, 得到新的特征函数
实际系统稳定性设计过程中, 只关心增益如何变化是不合理的, 因为一个好的系统对响应时间也有要求. 极点的位置能够直接反映一个系统的响应衰减或翻倍所需的时间, 对这个时间做限制, 也就是对极点位置做限制, 可以保证系统的响应不会太快或太慢.
- 具体来说极点离实轴越远, 响应减半或翻倍的时间越短, 因为极点在实轴上的分量表现为一个指数项, 当极点在实轴左边时, 这是一个指数衰减项; 当极点在实轴右边时, 这是一个指数增长项. 离实轴远, 指数的系数绝对值大, 变化就快, 如图:
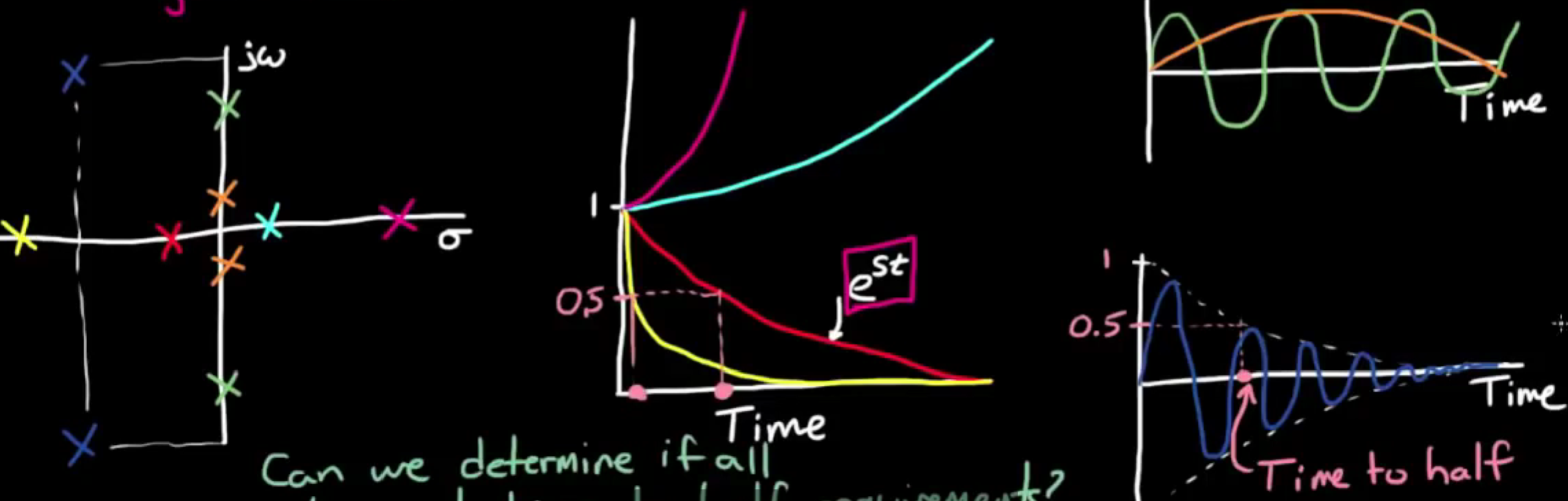
- 我们可以利用劳斯数组来判断一个系统的响应是否满足减半时间的需要。例如我们对减半时间有要求,在s平面上体现为极点必须在σ = -1的左边,而之前我们用劳斯数组,是来判断极点是否在jw轴,也就是σ = 0的左边。只需在特征方程中,将s代换为s-1,得到新的特征方程,再使用劳斯数组即可:

- 具体来说极点离实轴越远, 响应减半或翻倍的时间越短, 因为极点在实轴上的分量表现为一个指数项, 当极点在实轴左边时, 这是一个指数衰减项; 当极点在实轴右边时, 这是一个指数增长项. 离实轴远, 指数的系数绝对值大, 变化就快, 如图:
