系统稳定性 闭环系统的稳定性

1. 系统稳定性的定义: 稳定性时衡量一个系统的响应在受到干扰后恢复到零的趋势. / 对于稳定的系统, 有界的输入产生有界的输出. BIBO.
   
   用一个小球在不同地形下的位移举例:
   

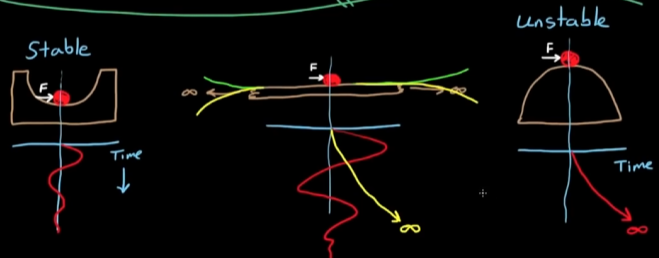
2. 一些关键参数如何影响系统稳定性? 有一个用飞镖的平衡性举的例子, 非常好: 【【中英字幕】Brian Douglas Control Theroy | 自动控制原理】 【精准空降到 02:37】
   主要内容是讲飞镖质量块和尾翼放置的位置如何决定飞镖的稳定性, 其中提到了飞镖刚好处于平衡的情况, 以及在这种情况下稍微移动尾翼的位置, 即可让飞镖变成稳定的系统(即使让飞镖平衡会花费很长时间). 然而我们不能让系统只要能稳定就行, 而是足够稳定, 能在限定时间内变稳定, 或者不至于让小的参数变化很大影响系统的输出.
   在此提出裕度 margin 的概念, 以及提出鲁棒的设计就等于有裕度.

3. 系统稳定性与响应灵敏度的取舍
   设计一个系统并不是稳定性越高越好, 因为稳定性过高的系统, 对输入也不会有太多响应. 例如一架过于稳定的飞机, 虽然飞行稳定, 但是不会对飞行员的操作产生响应, 因为它不想离开它的平衡点. 这并不是一架好飞机. (man !)

4. 开环控制系统: 不使用反馈来确定系统是否满足其期望状态.
   加上对反馈的比较之后, 系统变为闭环控制系统.
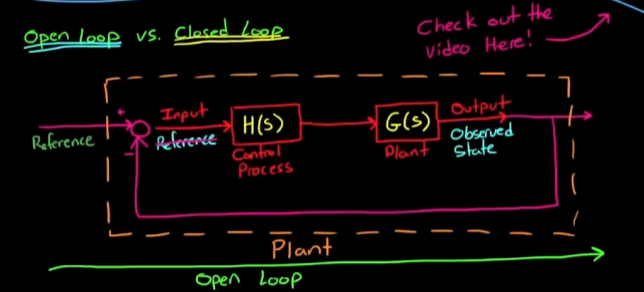
   但是一旦将闭环的过程包含在系统之中, 整个新的系统重新可以被看作开环控制系统:
   
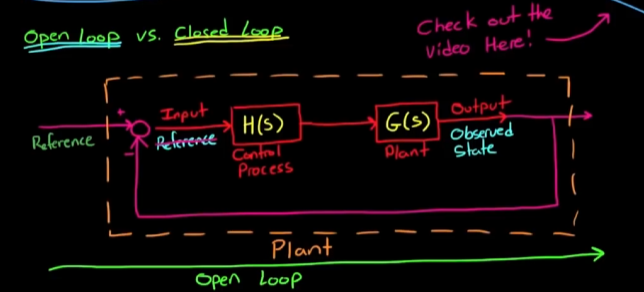
   也就是说, *闭环系统也可以被看作开环系统来进行进一步优化. *

5. 如何确定开环系统的稳定性? 观察系统的极点.
   当系统极点都在s平面的左半边的时候, 系统是稳定的, 因为当这样的系统通过Laplace逆变换变换回时域上, 当t->∞, 函数值趋于0, 这很容易证明.
   对于闭环系统, 我们仍然可以这样做, 即将闭环系统传递函数重写为开环系统的, 然后用计算机工具求其极点(计算方程的根). 但是传统实践中更多的是使用Bode图, 根轨迹 Root Locus, 劳斯判据 Routh-
   Hurwitz Criterion, 奈奎斯特稳定判据 Nyquist Stability Criterion, 等等方法来确定系统的稳定性.

6. 为什么要使用那些方法, 而不使用matlab?

   • 从前没有matlab和计算机的时候, 解决一个例如复杂的八阶多项式方程非常困难. 所以发明了一系列方法.
   • 我们不止需要知道系统是否稳定, 还需要知道如何设计系统, 使系统满足一系列性能指标, 而不仅仅只是”稳定”(如前所述, 只是稳定并不能解决问题). 所以我们需要了解设计和调制系统的方法.