根轨迹介绍与手绘根轨迹

根轨迹介绍

1. 对于一个控制系统，系统中可能存在一些未知参数，这些参数变化会导致系统极点位置变化。无论是设计系统还是优化系统，考虑这些参数变化带来会带来怎样的极点变化都是必要的。例如：
   
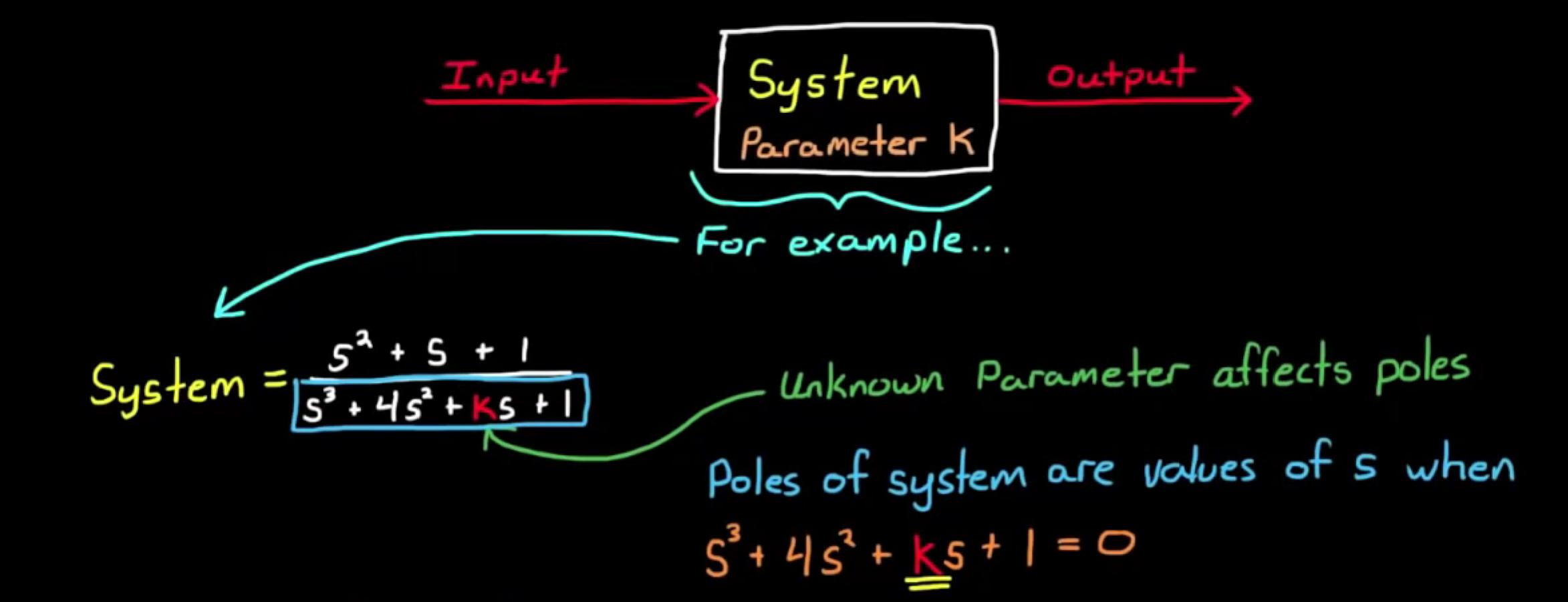
   其中k就是一个我们可以改变的参数，通过设计k，我们能设计出符合要求的系统，或用k的变化来模拟某些输入变化或扰动，从而得出系统的鲁棒性。

2. 当我们对k的取值进行连续的扫描，得出所有可能的极点并连点成线，我们就能得到k变化到极点位置变化的映射关系，极点位置变化连成的轨迹就是所谓的“根轨迹” Root Locus.
   

3. 我们强调极点, 是因为极点与系统稳定性直接关联. 虽然系统的激励响应需要用零点和极点共同表征, 但是谈到稳定性, 只需考虑极点, 并且极点决定了脉冲响应的基本模态, 例如震荡与否, 发散与否.

4. 在二阶系统中有一个概念是阻尼比 damping ratio, 它是一个归一化的数值, 当damping ratio = 0时, 系统没有阻尼, 做纯震荡运动; 当damping ratio >= 1时, 系统过阻尼或完美阻尼, 做指数衰减运动. 系统阻尼如何, 是可以通过极点的位置直接看出来的. 将极点与原点连线, 连线与实轴锐角夹角的cos值就是阻尼比, 如图:
   

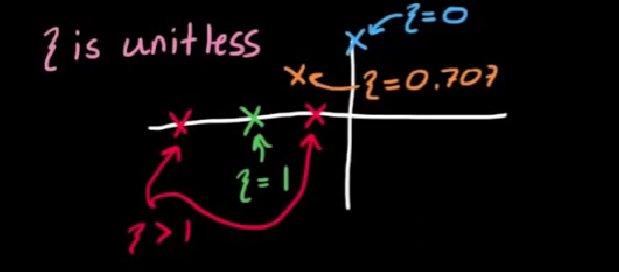
5. 系统设计的需求, 一般来说需求可以被量化为阻尼比, 固有频率, 衰减时间以及它们的组合:
   

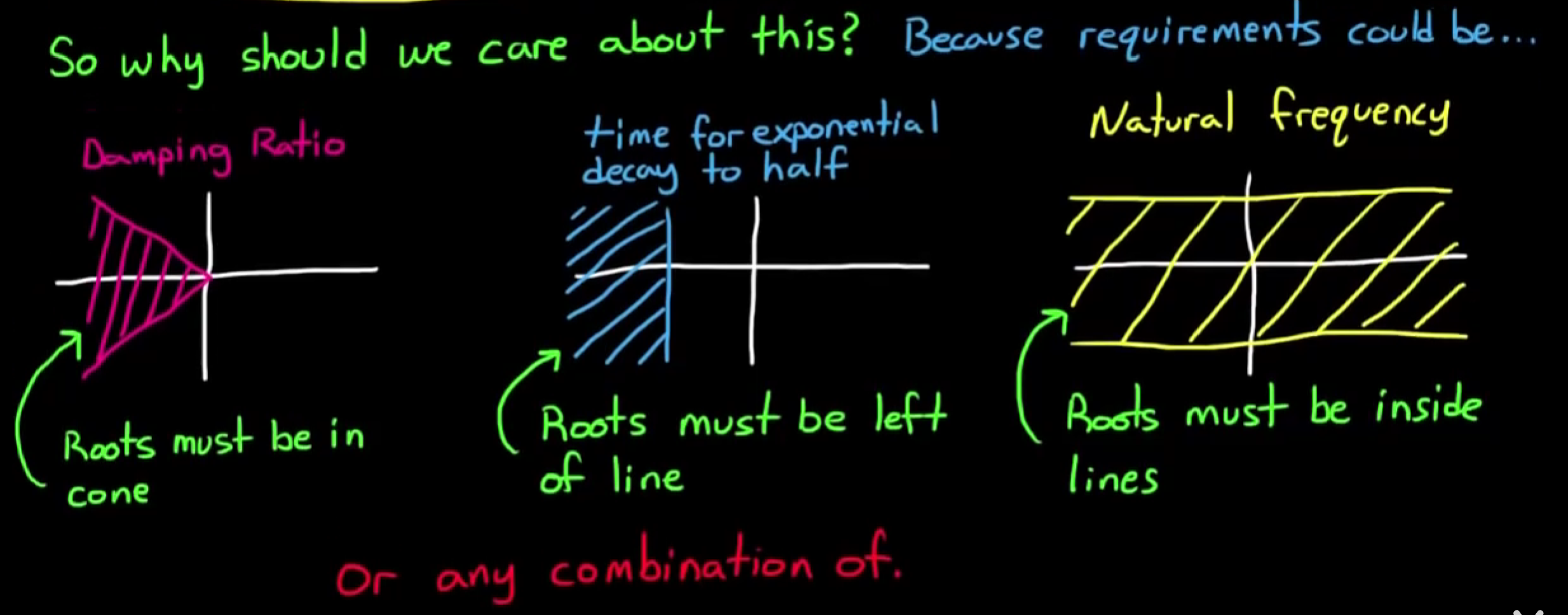
   • 例如我们设计系统时, 有一个参数可以改变, 而且对系统设计有阻尼比的要求, 则画出根轨迹, 考虑阻尼比, 即可选择合适的极点位置, 如图:
     
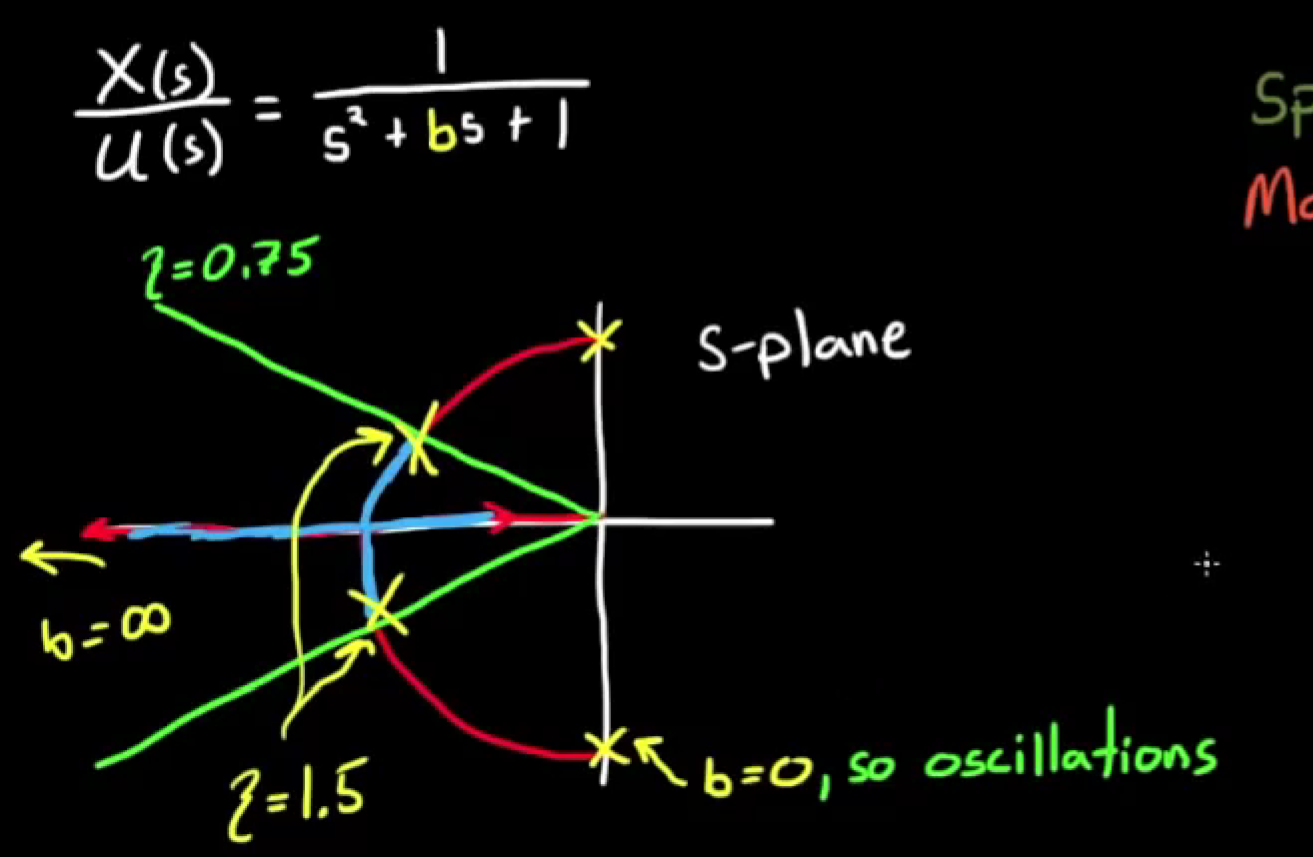
   • 考虑成本和其它因素, 我们可能会选择尽量靠近边界的极点作为设计目标, 但是当这个参数(如上图是b)因为一些实际原因(如温度)稍微变化, 或者其它位置的参数变化(例如s²的系数), 导致极点偏离理想位置, 离开了阻尼比的限制区域, 那就很坏了.
   • 从现实角度考虑, 此时我们可以重新设计系统, 再次使用根轨迹法,* 针对会随温度变化的参数来设计极点位置*, 使其在不同温度下使用还能保持性能; 或者给系统增加一个使用温度限制.

手绘根轨迹

• 为什么要学习手绘根轨迹? 而不是直接使用matlab画一个根轨迹?
  • matlab中的rlocus函数仅仅关心闭环增益对系统极点的影响, 即:
    
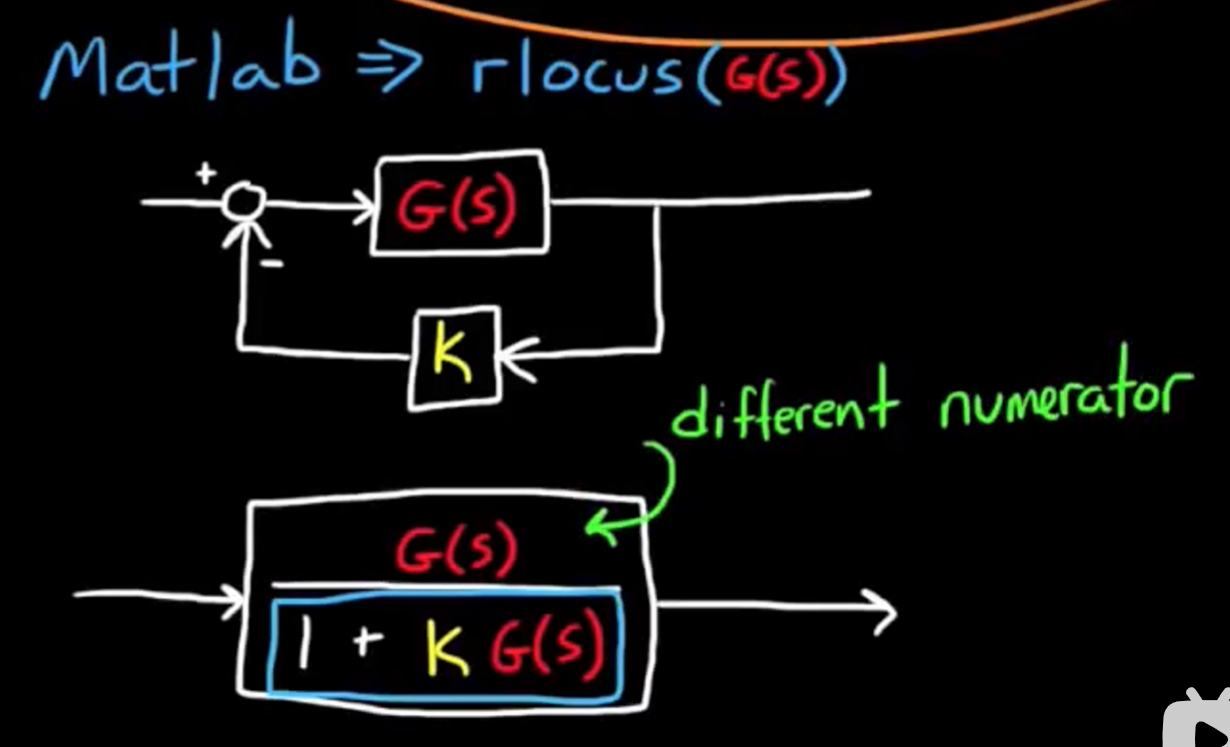
    并不关心系统内部参数变化的情况, 这种方法被称为传统根轨迹, 而我们之前一直讲的根轨迹法是能够考虑任意参数变化的, 这种方法被称为广义根轨迹.
  • 广义根轨迹可以通过重写特征方程的方式来转换为传统根轨迹的形式:
    
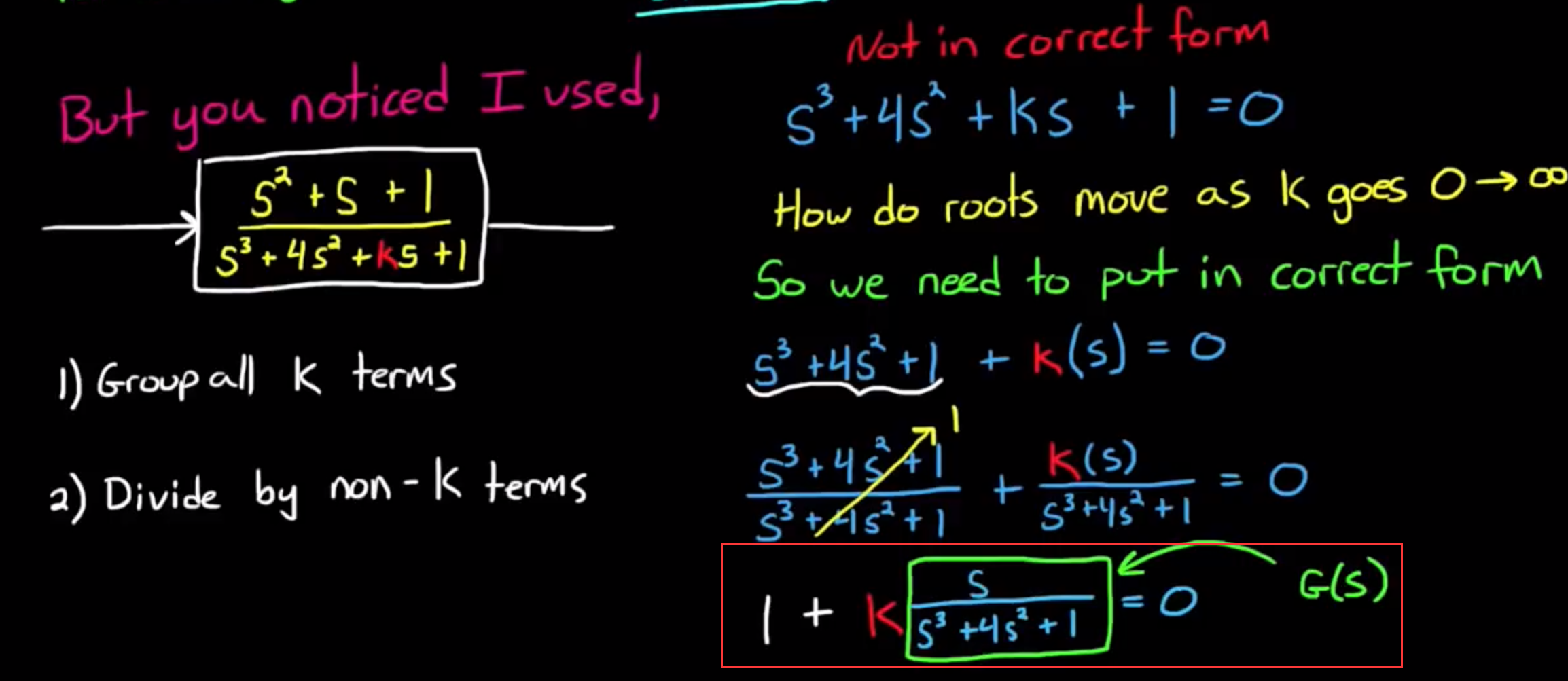
    上图中红框中的部分是重写后的特征方程, 找出不同参数K下特征方程的根, 就是根轨迹. 此时绿框中的部分是新的系统传递函数, 分析K作为任意变化的参数对原系统极点位置的影响, 等于分析K作为闭环增益对新系统极点位置的影响, 即有以下等效:
    
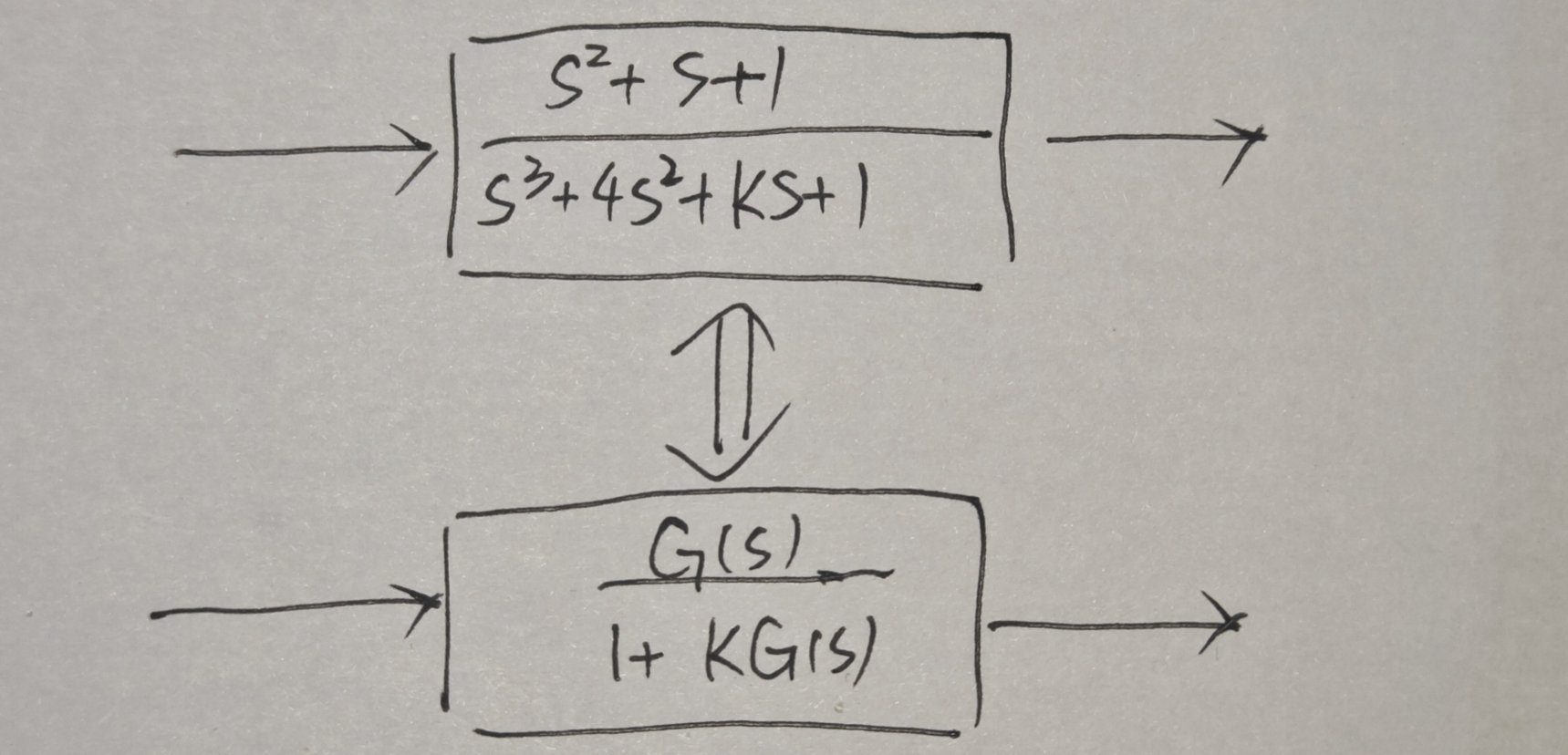
  • 鉴于matlab不能帮助我们直接解决问题, 我们需要学习这节课.
  • 而且学习手绘根轨迹, 也能帮助我们依靠直觉来估计一个参数变化对系统性能的影响.

手绘根轨迹的规则

参数的变化导致根轨迹的移动, 其这种移动遵循一系列的规则如下:

• 首先让我们将特征方程写成这样:
  

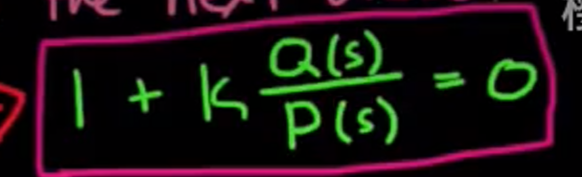
1. rule 1 有n条根轨迹, n是Q(s)和P(s)中幂次较高的一个
2. rule 2 当K从0增长到∞, 特征方程根从极点的位置移动到0点的位置.

• 前两条综合起来考虑, 当第二条成立的时候, 意味着任何一个极点和零点都有与之匹配的零点和极点, 并且它们中间有一条根轨迹, 那么P和Q中更高次就决定了根轨迹的数量, 毕竟高次幂代表更多个零点或极点.
• 特征方程的根为什么是从极点移动到零点的? 因为当我们将特征方程写成这样时:
  
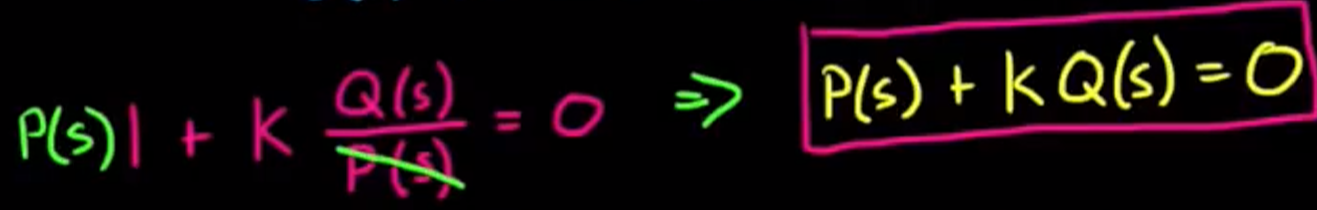
  k = 0, 则特征方程根确实是P的根, 也就是极点;
  k = ∞时, 特征方程根与P几乎没有关系了, 而是等于Q的根, 也就是零点;
  k取值在这中间的情况是根逐渐从极点向零点移动的过程.

3. rule 3 复数根永远以共轭形式出现, 详情参考前面提到的, 二次方程判别式产生复数根时必定是共轭复数.

4. rule 4 根轨迹不会与自己相交, 这意味着一个s值不会对应一个以上的k值. 当然两个根轨迹之间有相交是没问题的.

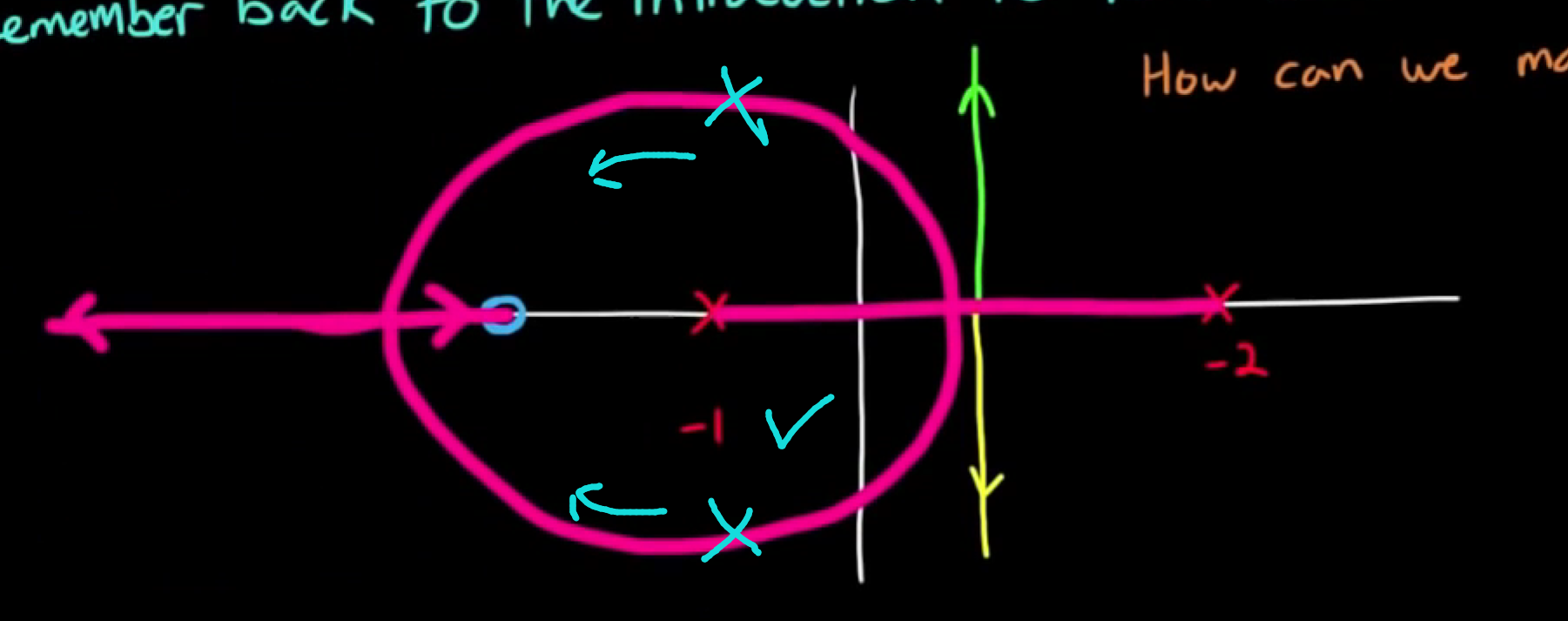
5. rule 5 从右往左数, 给所有的零点和极点编号, 则根轨迹的一部分永远在奇数点的左边, 看图更好理解:
   
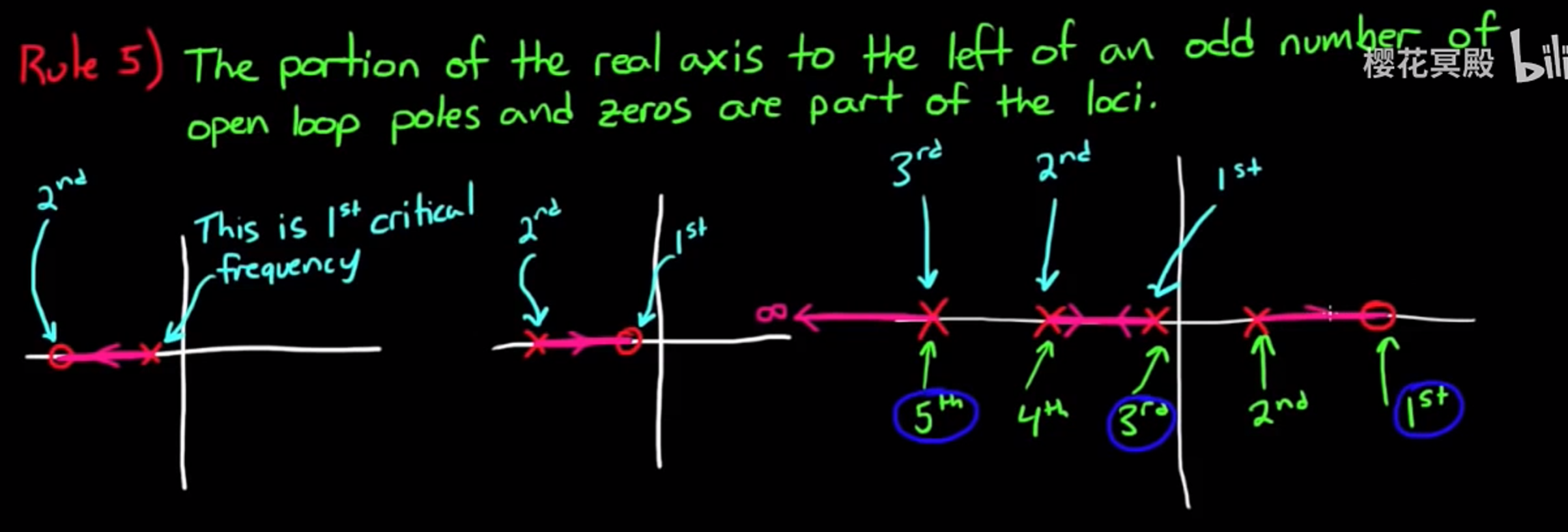
   若有五个极点和零点(或者称为”关键频率”), 从右边开始, 第一个零点和极点配对,* 根轨迹在一号点左边*; 三号点和四号点的轨迹汇拢到一点(后续如何走在接下来会讲, 仍然满足这条规则), 根轨迹在三号点左边; 五号极点轨迹指向无穷远, 去”寻找”无穷远处的零点, 根轨迹仍然在左边.

6. rule 6 两个根轨迹聚集在一起要离开实轴的时候, 必定是以90°离开; 轨迹进入实轴的时候, 必定是以90°进入.

7. rule 7 如果零点或极点数量不够, 不足以全部匹配, 则会有无穷远处的极点来匹配零点, 或者不匹配的极点出发匹配无穷远处的零点. 这一条规则对rule 2和rule 5做了进一步补充. 用图片来说明更好理解:
   

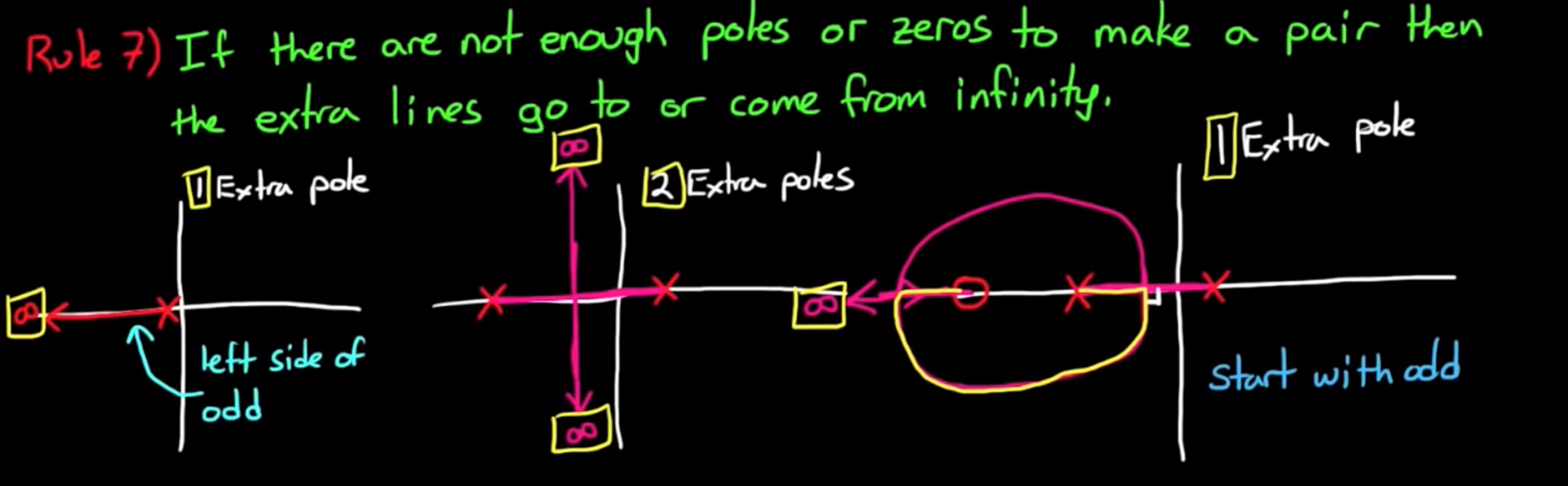
   • 看第二个图, 首先是根轨迹的一部分在奇数点左侧, 也就是第一个点左侧, 两个多余的极点发出的轨迹往中间汇集, 并以90°离开实轴前往无穷远.
   • 看第三个图, 两个极点发出的根轨迹仍然先汇集在一起, 90°离开实轴, 但是绕了一个大弯子, 最后有一条根轨迹指向实轴上的零点, 另一条根轨迹指向无穷远. 为什么不是极点直接指向零点? 因为根轨迹要满足一个约束, “轨迹的一部分在奇数点的左侧“, 由于零点是奇数点, 所以它的左侧必须有根轨迹, 根轨迹必须从左侧绕回来, 而不是直接从右侧进入.
   • 接下来有一个疑问, 如何知道那些指向无穷远的根轨迹的方向? 什么时候是90°垂直于实轴, 什么时候是180°, 与实轴反向? 还有没有其它方向? rule 8 即将为我们解答这些疑问.

8. rule 8 指向无穷远或从无穷远处来的根轨迹会逼近渐近线, 渐近线发出的位置和角度取决于多余零/极点的数量和位置. 简单来说, 第q根渐近线的角度 = 180 * {[(q-1)*2 + 1] / 多余点个数} , 渐近线发出位置 = 多余点的重心, 看图更清晰:
   

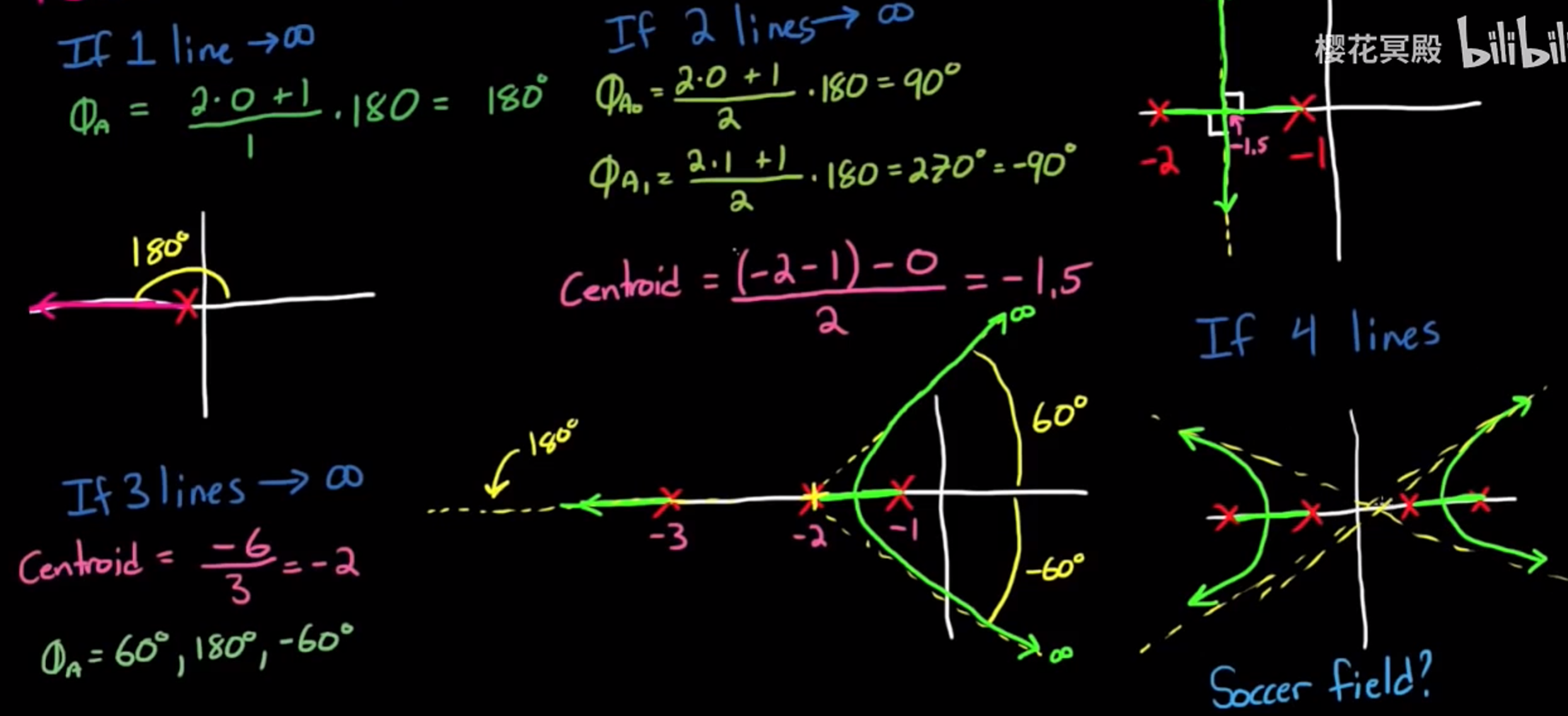
   • 可见, 有一个多余点, 则第一根渐近线与实轴夹角180°, 重心在唯一一个极点上; 有两个多余点, 则渐近线分别与实轴夹角90°和-90°, 重心在两极点连线中点; 有三个多余点, 则渐近线分别与实轴夹角60°, 180°, -60°, 重心通过 (σ1 + σ2 + σ3) / 3 来计算; 有四个多余点同理, 以此类推.
   • 这条规则说明了指向无限远的根轨迹离开实轴后的走向, 还是比较有规律可循的.

9. rule 9 如果有两个以上指向无穷的根轨迹, 那么在根移动的时候, 所有根的实坐标相加是一个常数. 看图更好理解:
   
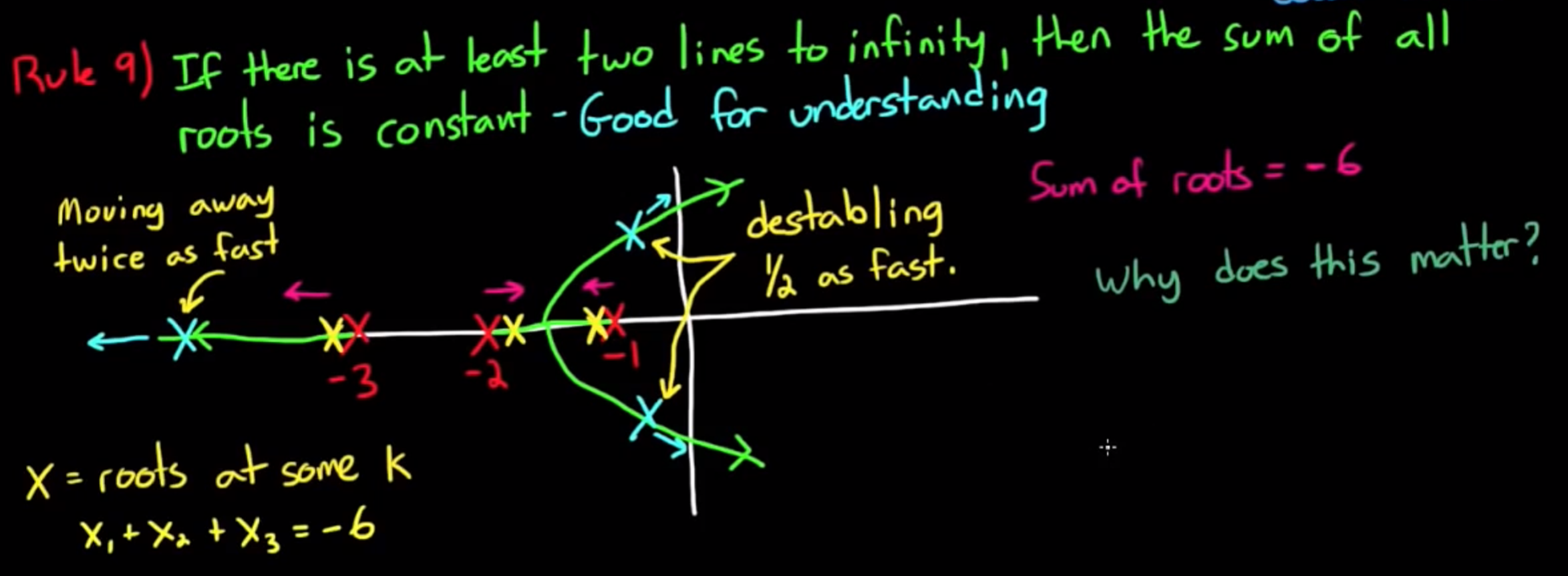
   例如上图的根轨迹, 我们可以知道, 当改变系统增益时, 让左边的实根变稳定的速度是让右边两个复数根变得不稳定的速度的两倍, 这可能是一个有用的知识.

10. rule 10 之前所讲的都是将k从0到正无穷遍历, 如果想让k从0到负无穷遍历, 则将 rule 5 反过来, 即”根轨迹的一部分永远在奇数点的右边“, 如图:
    

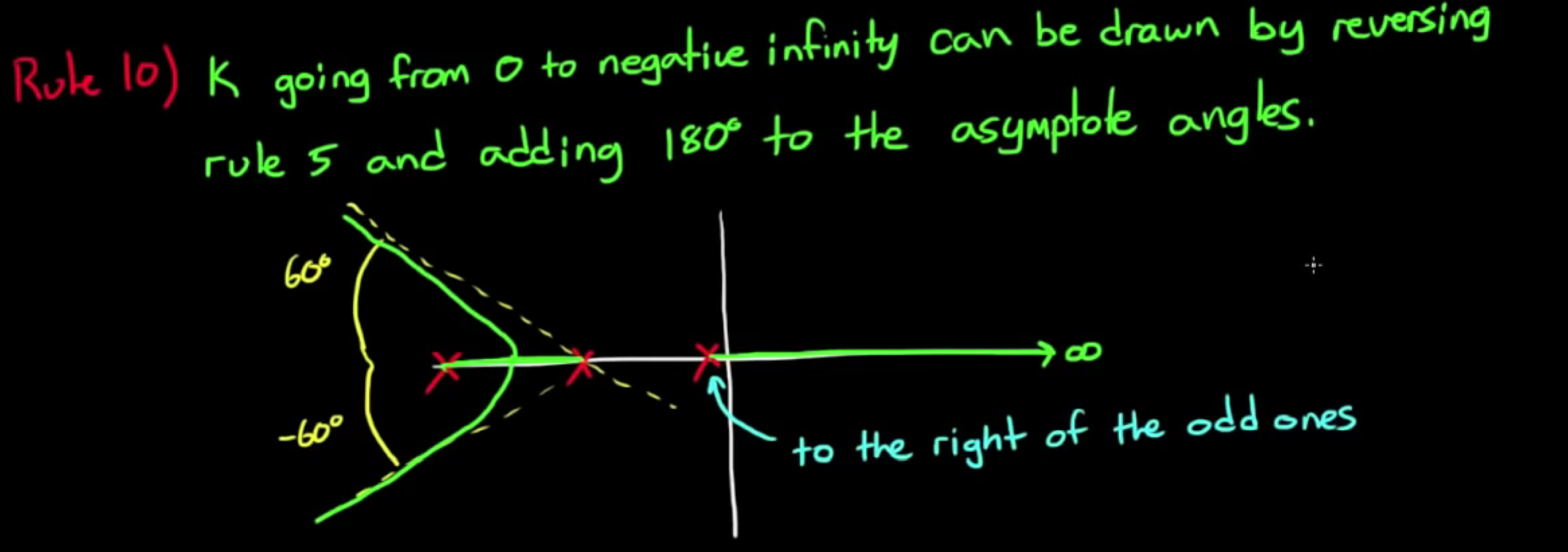
• here is an example~
  • 有一个开环控制系统, 加上比例控制系统之后, 根轨迹如图, 可以发现单纯加一个闭环增益, 并不能使系统达到稳定的状态. 如下图
    
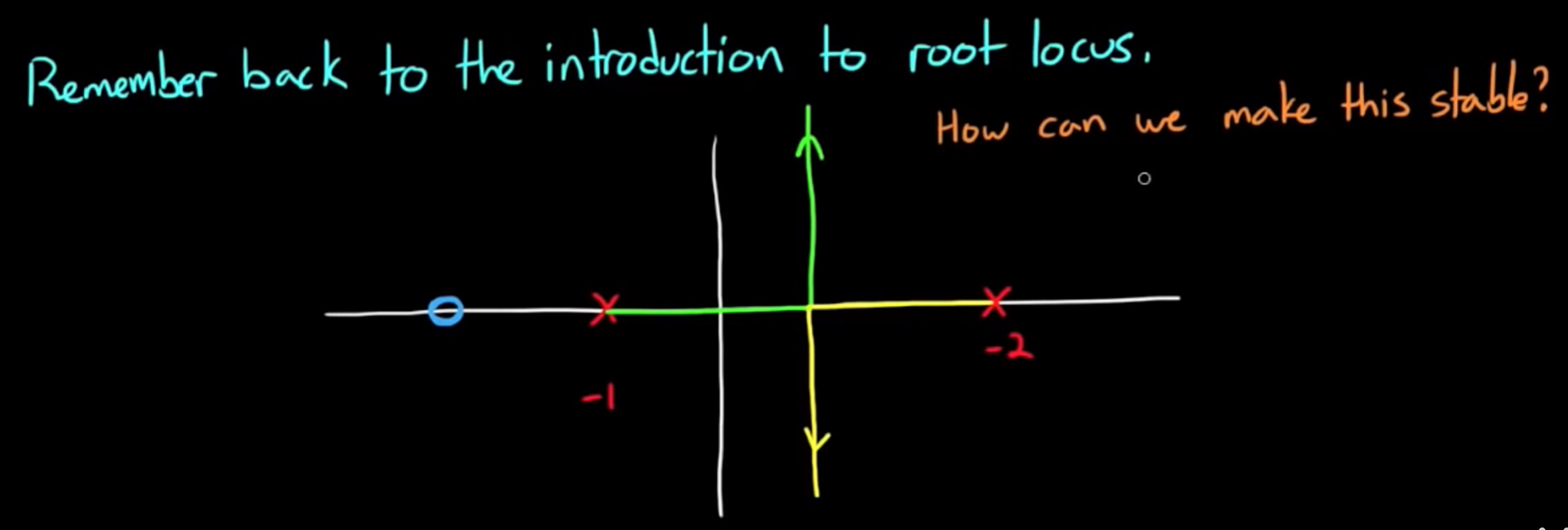
  • 如果我们选择再增加一个极点呢? 无论这个极点加到什么位置, 由于渐近线角度问题, 还是没法让最右边极点发出的根轨迹进入左半区; 无论增加几个极点, 都是殊途同归.
  • 那么加入零点呢? 在左半区加入一个零点, 首先能保证一个极点发出的根轨迹一定会落在左半区, 其次还能改变渐近线角度, 使指向无穷远处的根轨迹最终朝向实轴反方向, 这样就一定有左半区的根. 如下图:
    
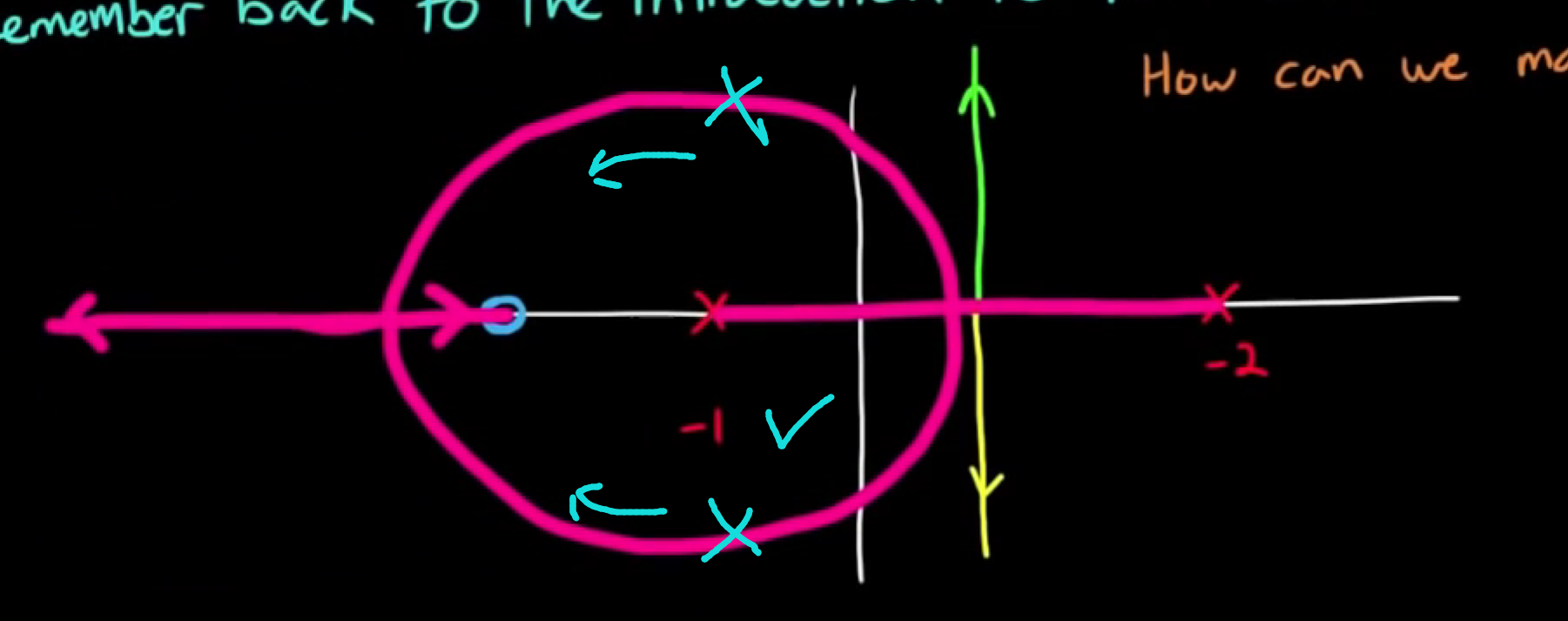
  • 离开根轨迹图, 从数学和系统的角度考虑, 加入一个零点s + 3, 实际上是加入了一个微分控制器, 与先前加入的比例控制共同构成了PD控制器.
    
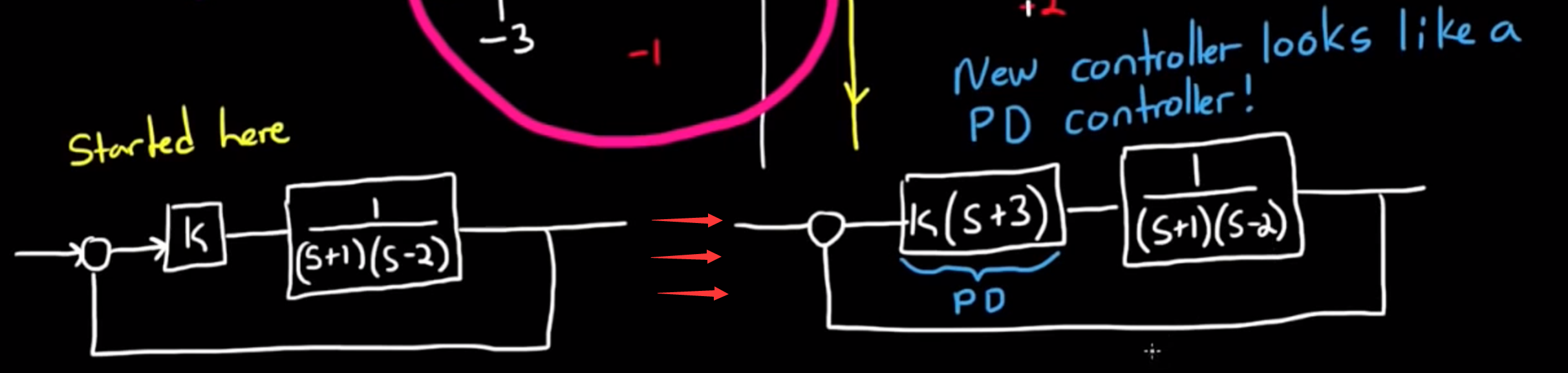
  • 这也与我在实际控制中体验到的一致, 只用比例控制几乎没法很好控制一个电机, 但是加上了微分项, 控制就会变得很好.