Nyquist稳定准则

我们为什么需要Nyquist判据？

1. 假设有开环系统如下：

   

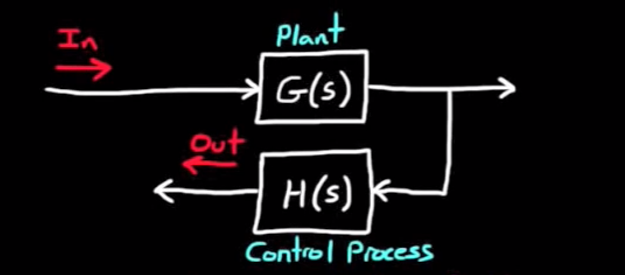
    那么可以轻松得到开环系统函数 = G(s)*H(s), 并且其零点和极点很好分析, 是G(s)的零极点并上H(s)的零极点.

2. 但是若将系统变为闭环控制, 如下:

   

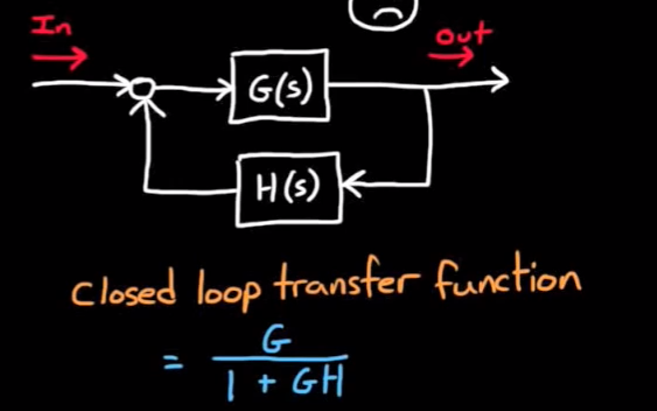
    此时系统特征方程就变成了 1 + GH, 此时特征方程的根就很不好分析, 因为 + 1 移动了零点和极点. 对于没有计算机程序辅助的时候, 解出这个特征方程可能异常困难. 例如用matlab画出随机的GH以及GH + 1的零极点图:

   

   

   

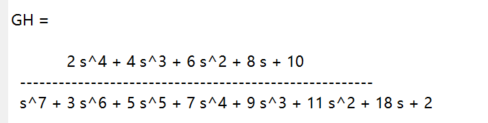
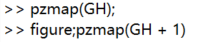
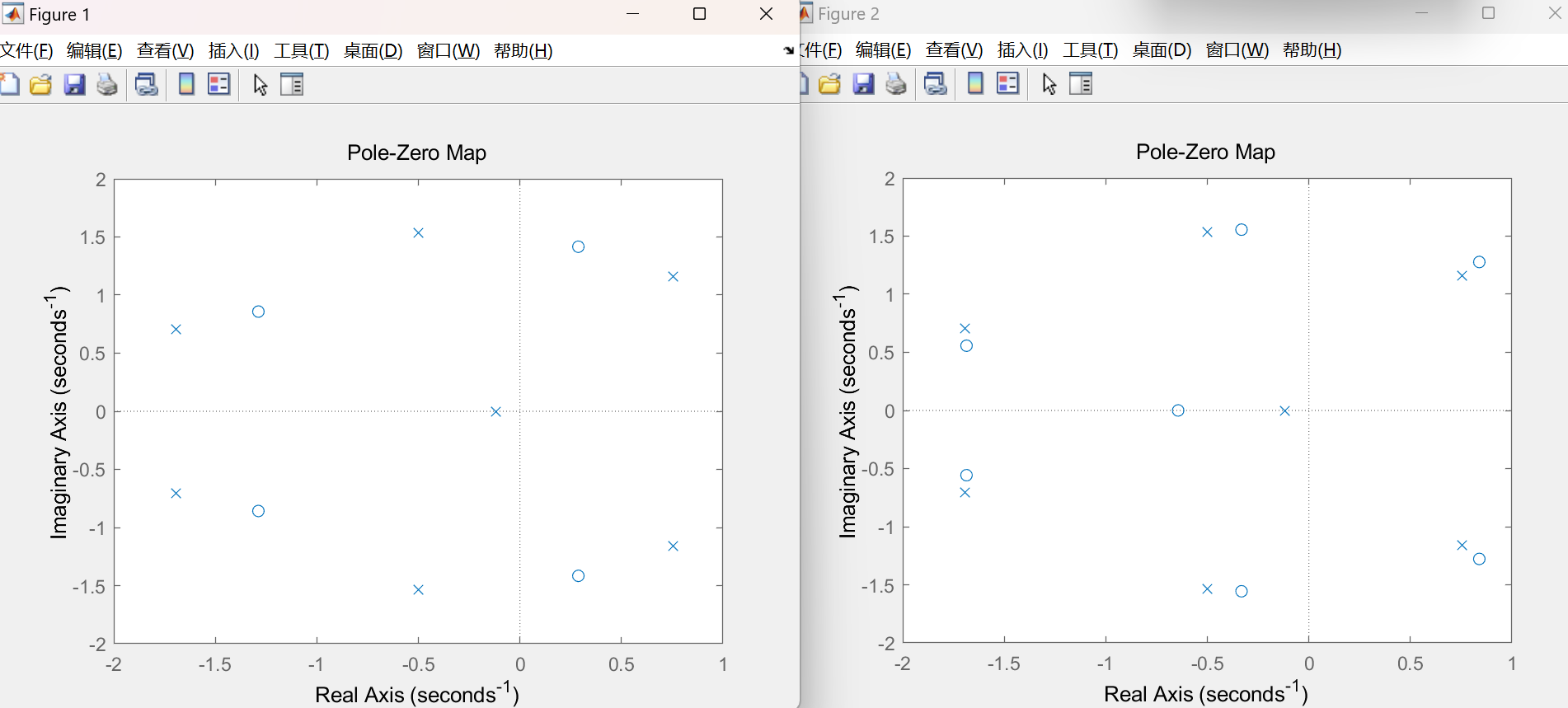
    可以看到* GH 和 GH + 1 的零极点之间不存在明显的关系*.

3. 我们有没有可能用开环系统的稳定性来判断闭环系统的稳定性呢? Nyquist稳定准则为我们提供了方法. 只需要按照一定规则画出开环系统的Nyquist图, 就可以判断闭环系统的稳定性, 以及得到稳定裕度. 用上面例子的系统函数, 画出 GH 和 GH + 1 的Nyquist图如下:

   

   

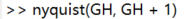
    可以看到两者Nyquist图是平移关系. 如果我们能从开环系统Nyquist图中得到稳定性信息, 则就能不用考虑闭环系统零极点的移动情况而直接得出闭环系统的稳定性信息.

如何得到Nyquist图: 柯西幅角原理

1. 当我们有一个系统函数, 在s域上取一点并代入, 例如将(1, j)带入系统 (s + 1) / (s + 2), 能得到 0.7 + 0.1j, 放在s平面上就是(0.7, 0.1), 这是一个新的点, 这个 取点->带入系统函数->在s平面上得到新点 的过程, 称为映射 mapping. 让我们把映射后的点放在和s平面一样的平面上, 但是称为w平面, Nyquist图就是通过映射, 在w平面上画出来的, 不过不是任意在w平面上的映射曲线都是Nyquist图, 后面我会提到.

2. 柯西幅角原理:

    - 当我们做如上所述映射的时候, 会发现一个规律:

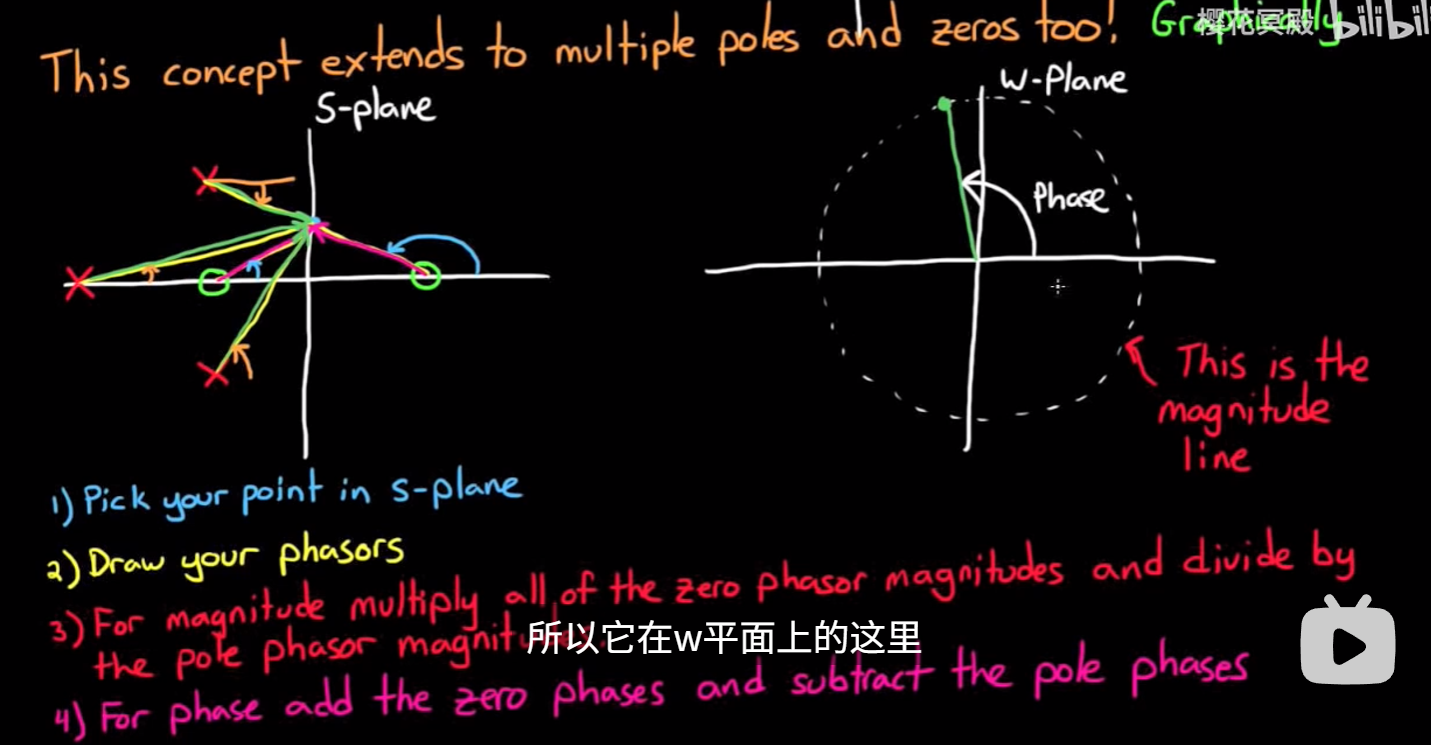
        1) 原点指向w平面上映射点的矢量的夹角, 或者说相位, 等于原s平面上系统零点指向被取点的矢量的相位之和, 减去原s平面上系统极点指向被取点的矢量的相位之和;

        2) 矢量的幅度, 即长度, 等于原s平面上系统零点指向被取点的矢量的幅度之积, 除以原s平面上系统极点指向被取点的矢量的相位之积.

    - 说起来很绕, 建议看Brian原视频的有图像的推导, 本人能力有限, 只能表达成这样: 【【中英字幕】Brian Douglas Control Theroy | 自动控制原理】 【精准空降到 05:12】 https://www.bilibili.com/video/BV1WT4y1M7rm/?p=26&share_source=copy_web&vd_source=44cc7f69ddf80fe5bcd5d6df9537b058&t=312

    - 具体执行步骤:

        1) s平面上挑选点

        2) s平面上画出所有从零极点指向被选取点的向量: p1, p2, p3…(从极点出发的向量) \ z1, z2, z3…(从零点出发)

           

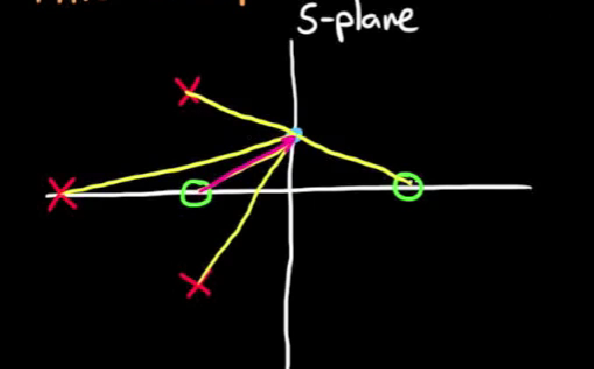
        3) 对于w平面上从原点指向映射点的向量, 幅度 = (|z1|*|z2|*|z3|*…) / (|p1|*|p2|*|p3|*…); 相位 = (Φ(z1) + Φ(z2) + Φ(z3) + …) - (Φ(p1) - Φ(p2) - Φ(p3) - … ).

        4)

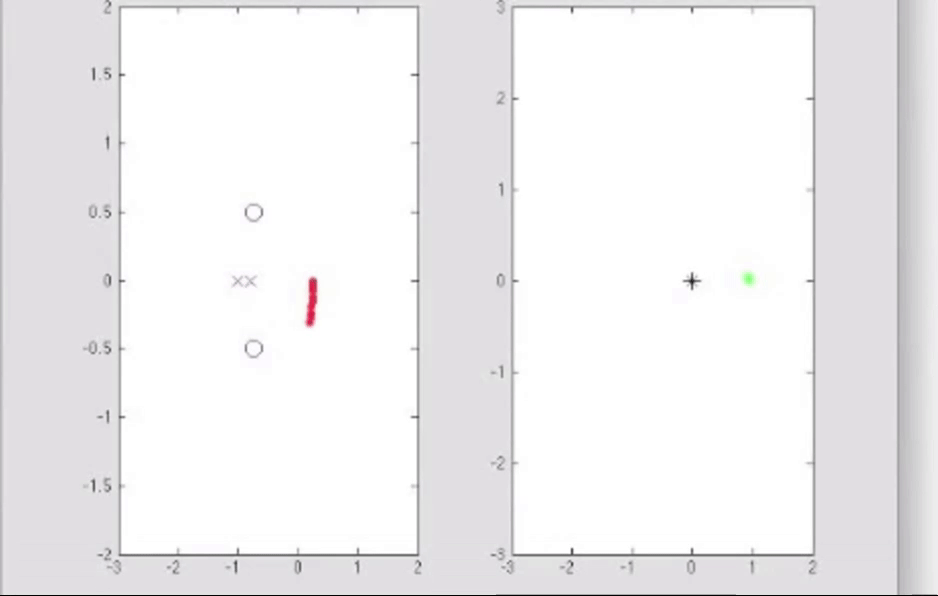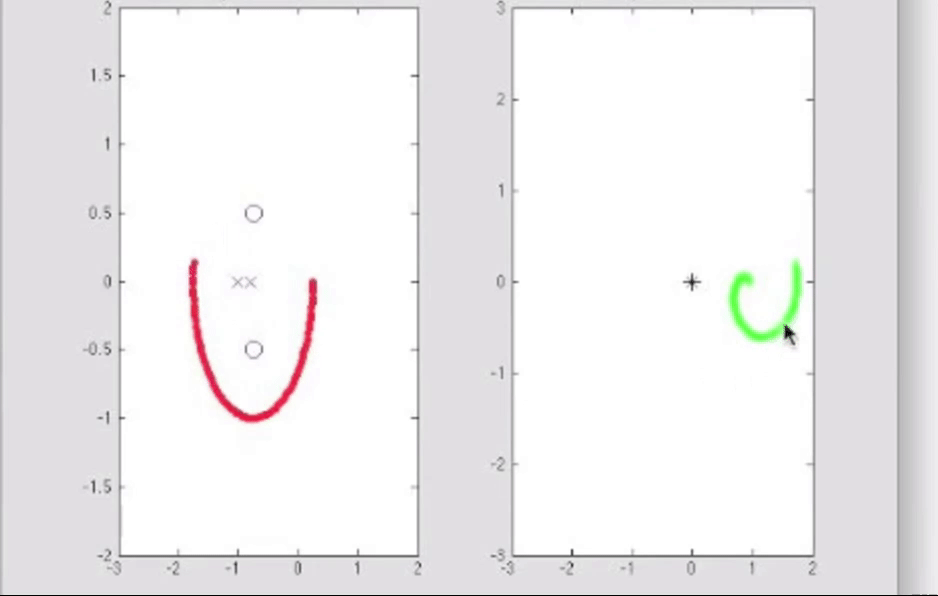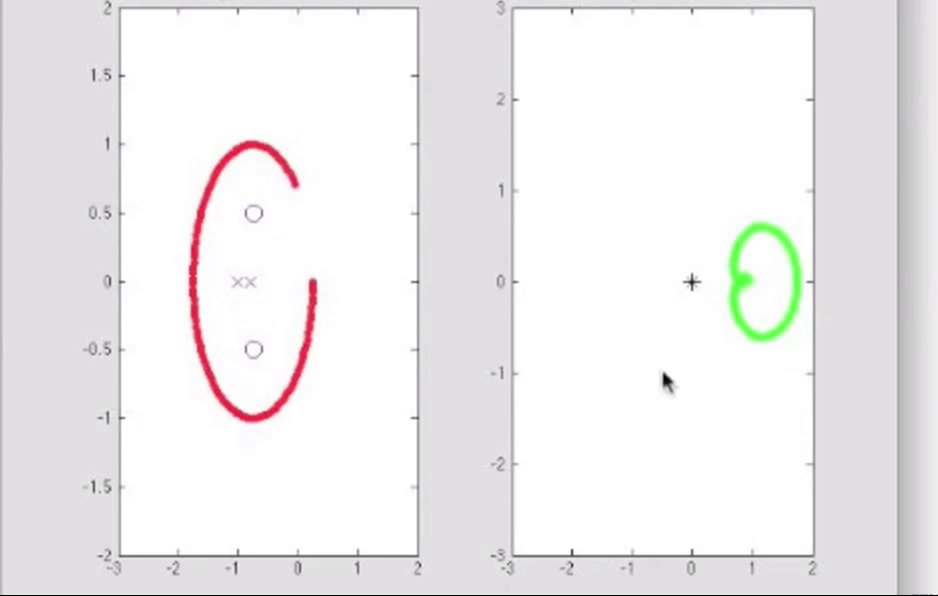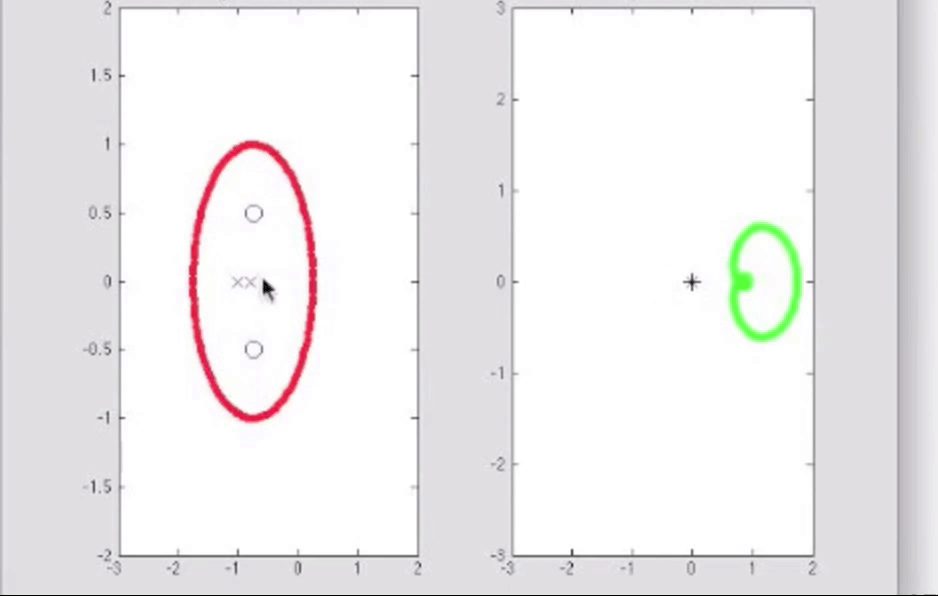
5. 柯西幅角原理的matlab演示, 我认为很有必要看: 【【中英字幕】Brian Douglas Control Theroy | 自动控制原理】 【精准空降到 07:15】 https://www.bilibili.com/video/BV1WT4y1M7rm/?p=26&share_source=copy_web&vd_source=44cc7f69ddf80fe5bcd5d6df9537b058&t=435

6. 由于有柯西幅角原理, 特别是关于相位计算那一部分的, 如果我们选取一条只围绕一个零点的闭合曲线, 那么那段曲线的映射就会是围绕原点一周的闭合曲线, 毕竟相位大体上有360度的变化; 类似地, 选取一条只围绕一个极点的闭合曲线, 映射曲线也会是绕原点一周的, 但是是沿着闭合的反方向, 毕竟相位是相减的关系, 例如s平面上曲线顺时针闭合, w平面上曲线逆时针闭合:

   

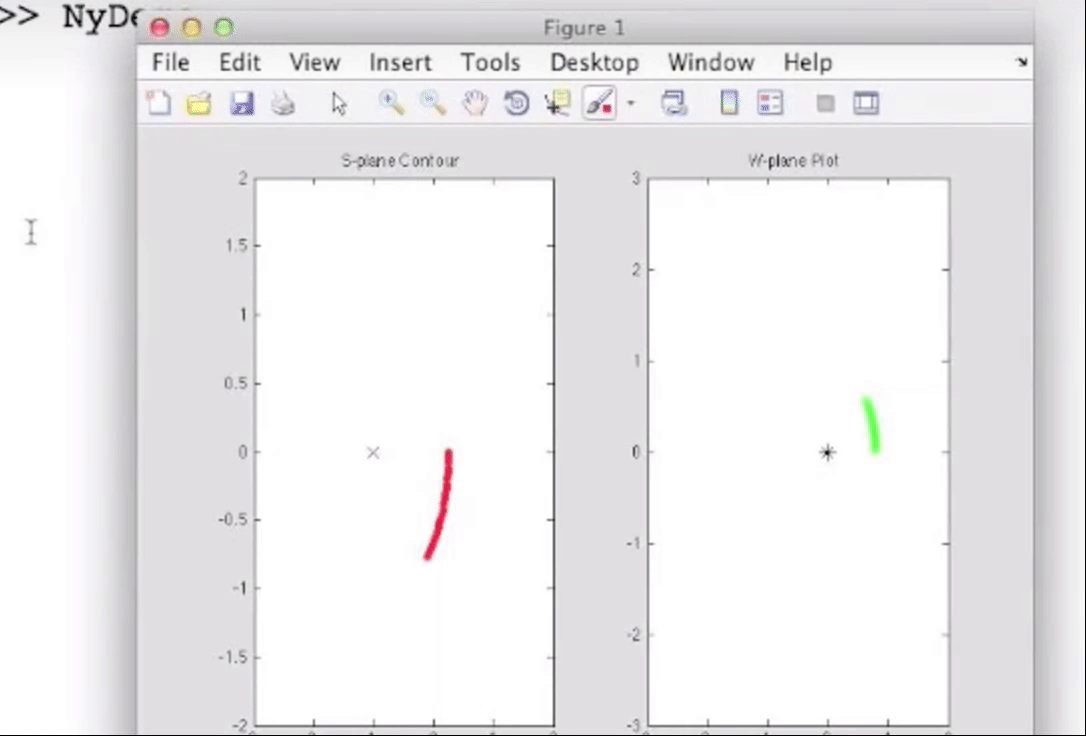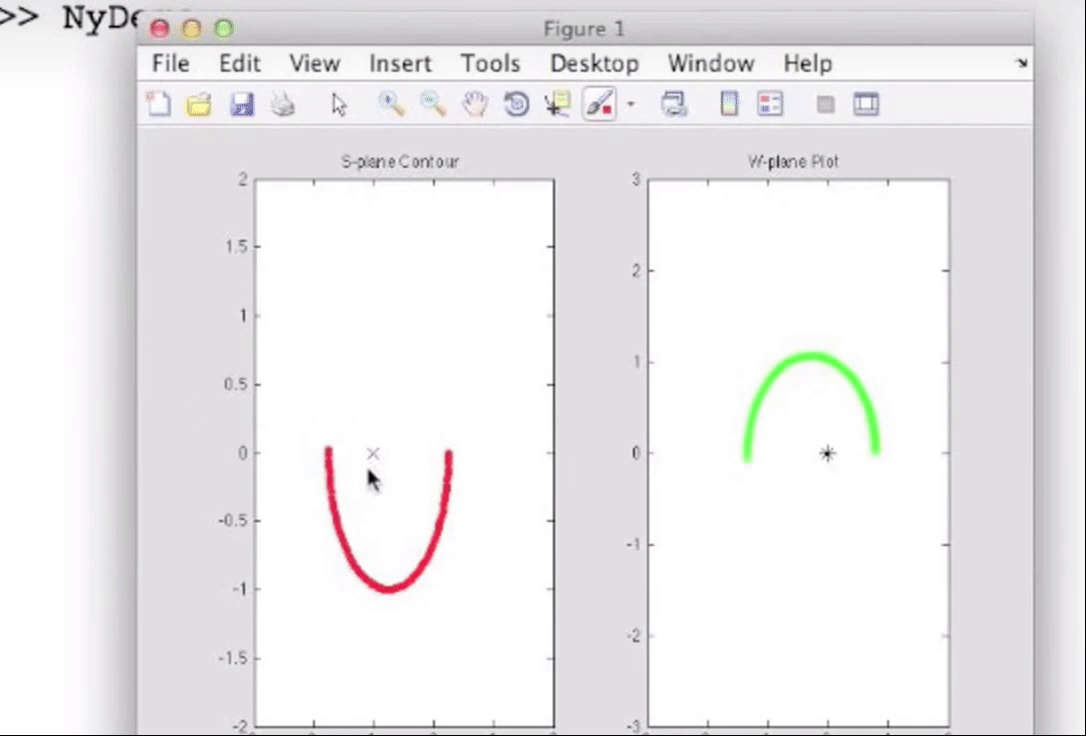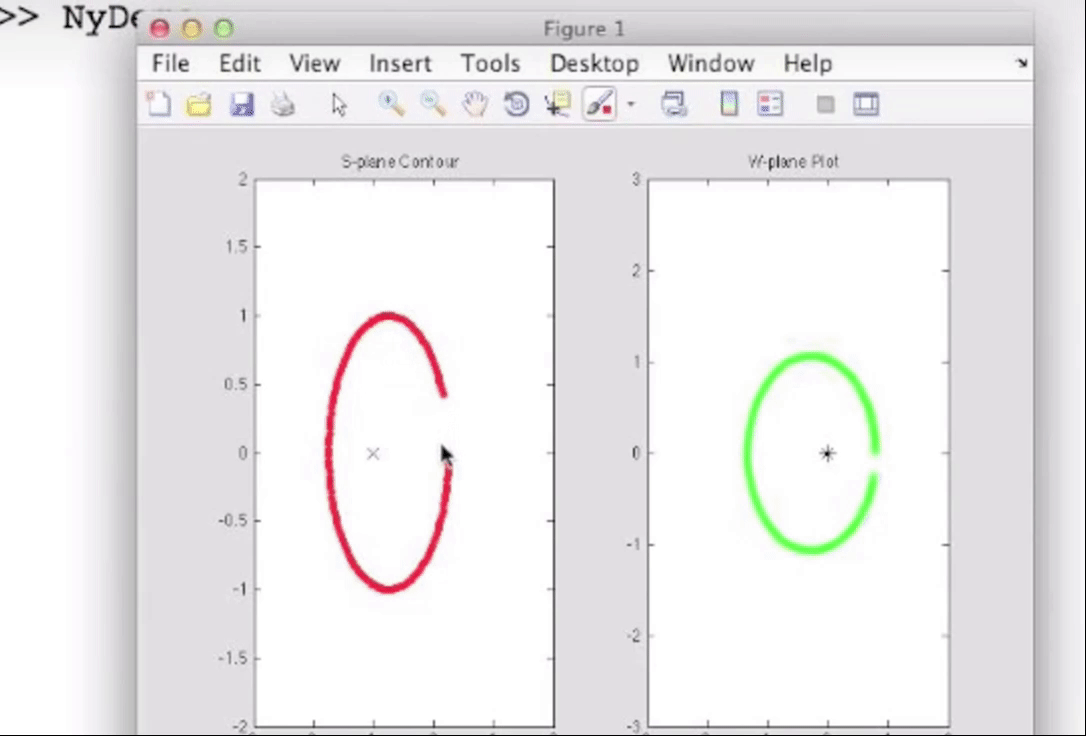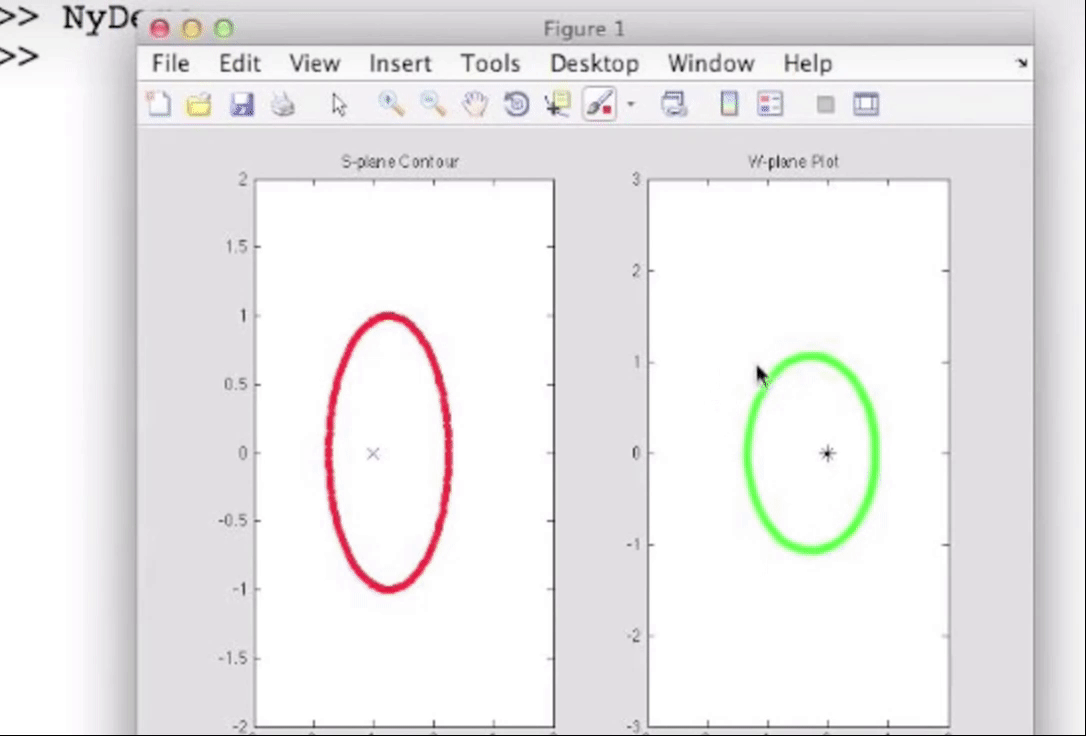
    如果只包含两个零点或极点, 那么就绕两周, 因为相位有720度的变化;

   

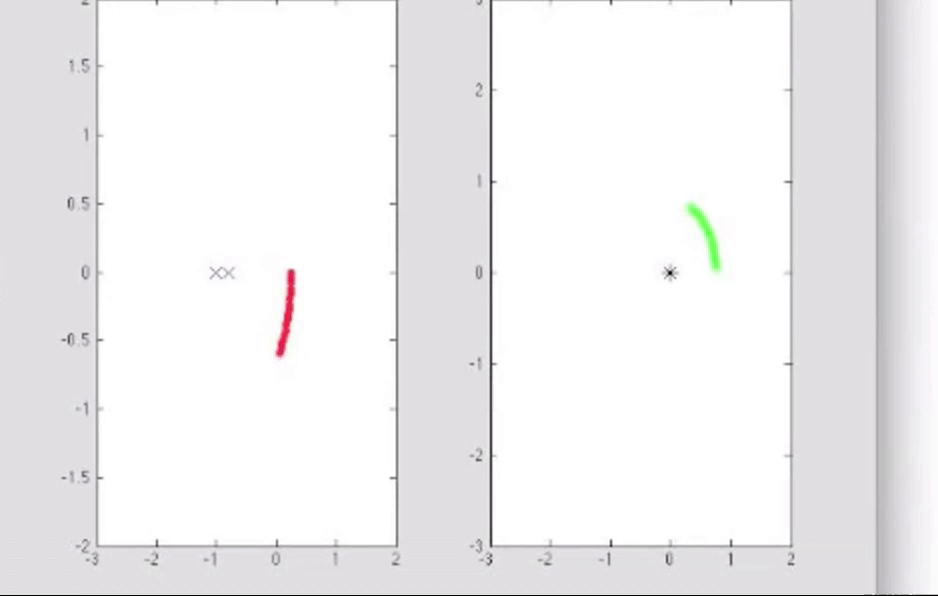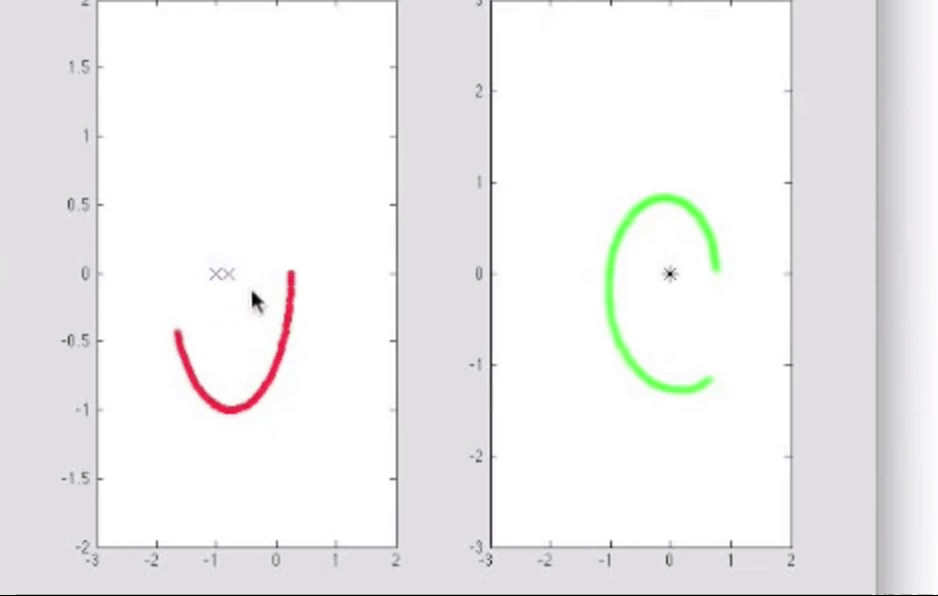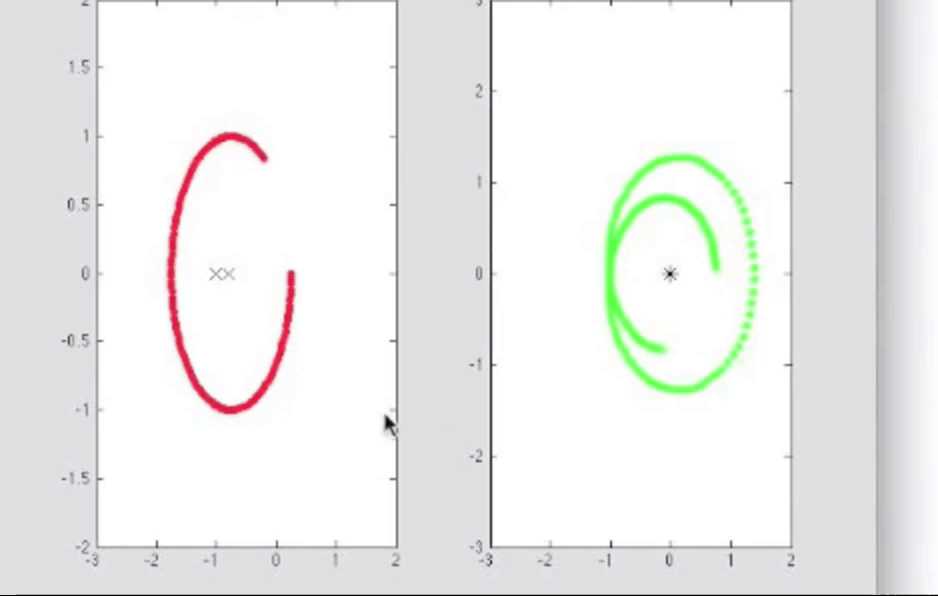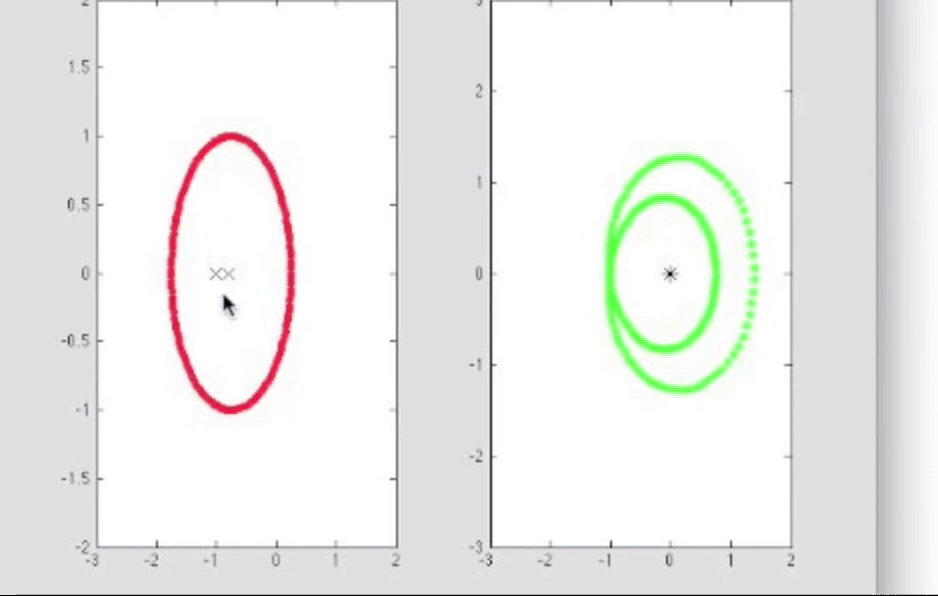
    如果选取一条包含同等数量的极点和零点的闭合曲线, 那么在w平面上的映射曲线绝不可能环绕原点一周, 最多有一些很接近的轨迹, 因为包含同等数量的零点和极点意味着相位变化存在抵消.

   

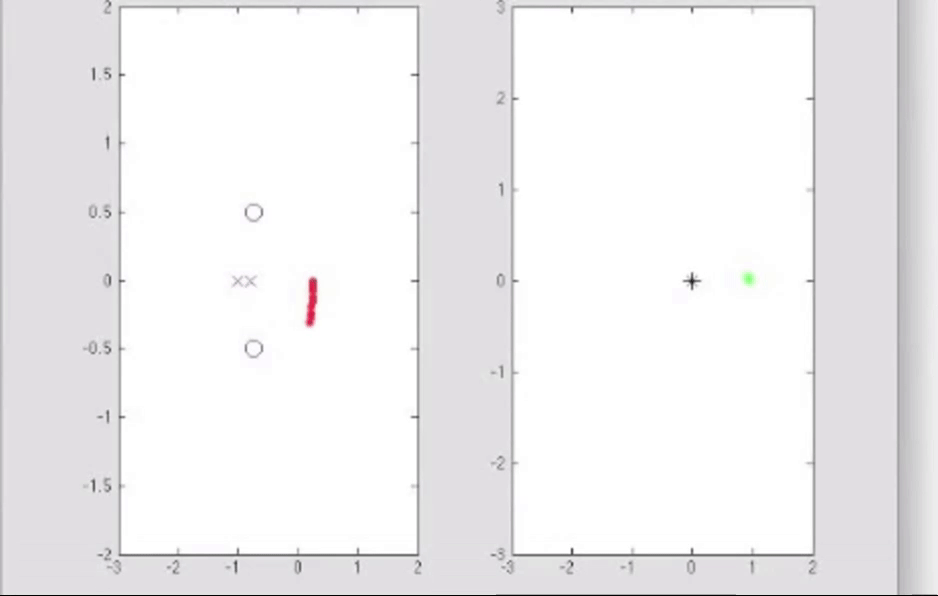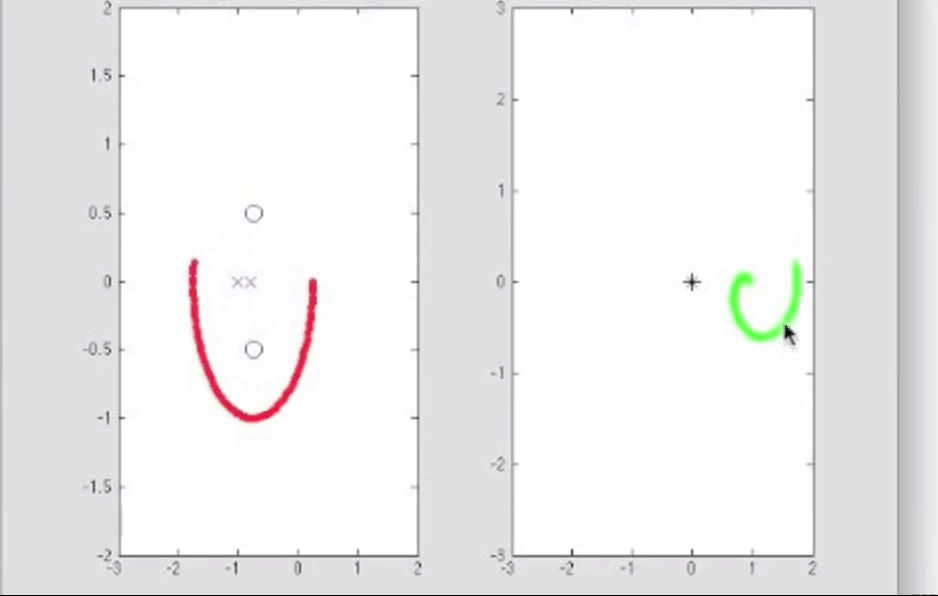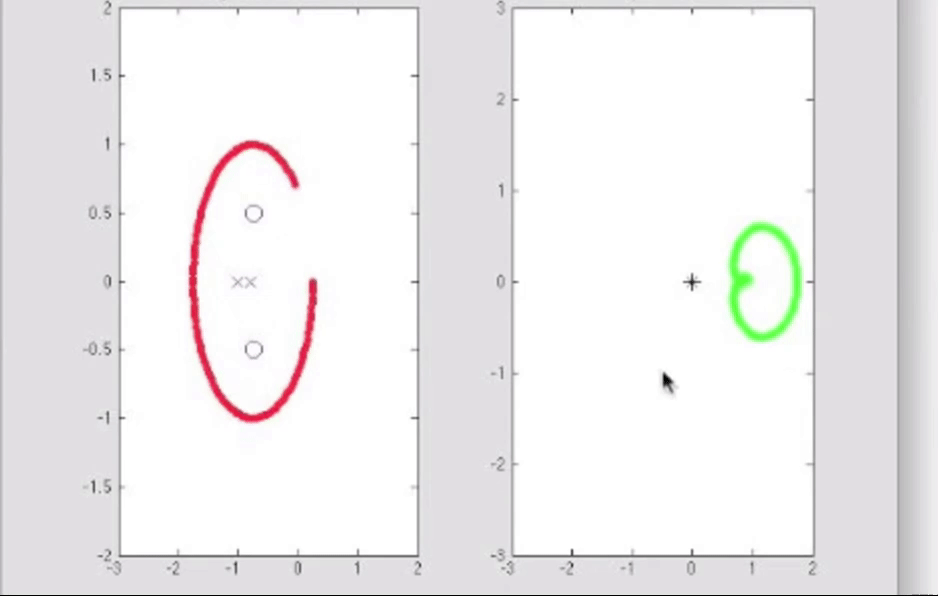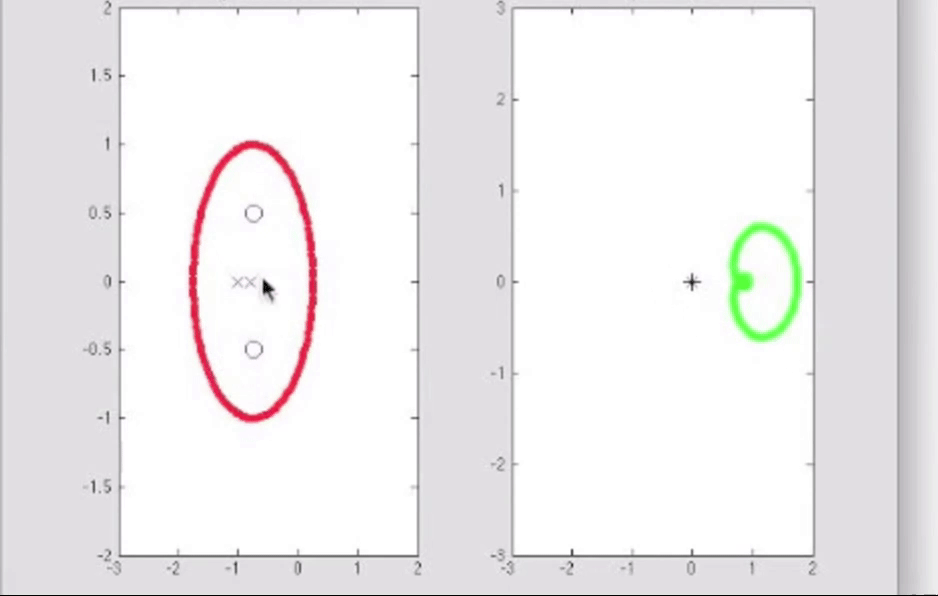
    再举例如下: 看红色轨迹, w平面中顺时针绕原点一周, 则表明s平面中的红色顺时针闭合曲线中, 零点比极点多一个; 看蓝色轨迹, w平面中逆时针绕原点两圈, 表面s平面中蓝色顺时针闭合曲线中极点比零点多两个

   

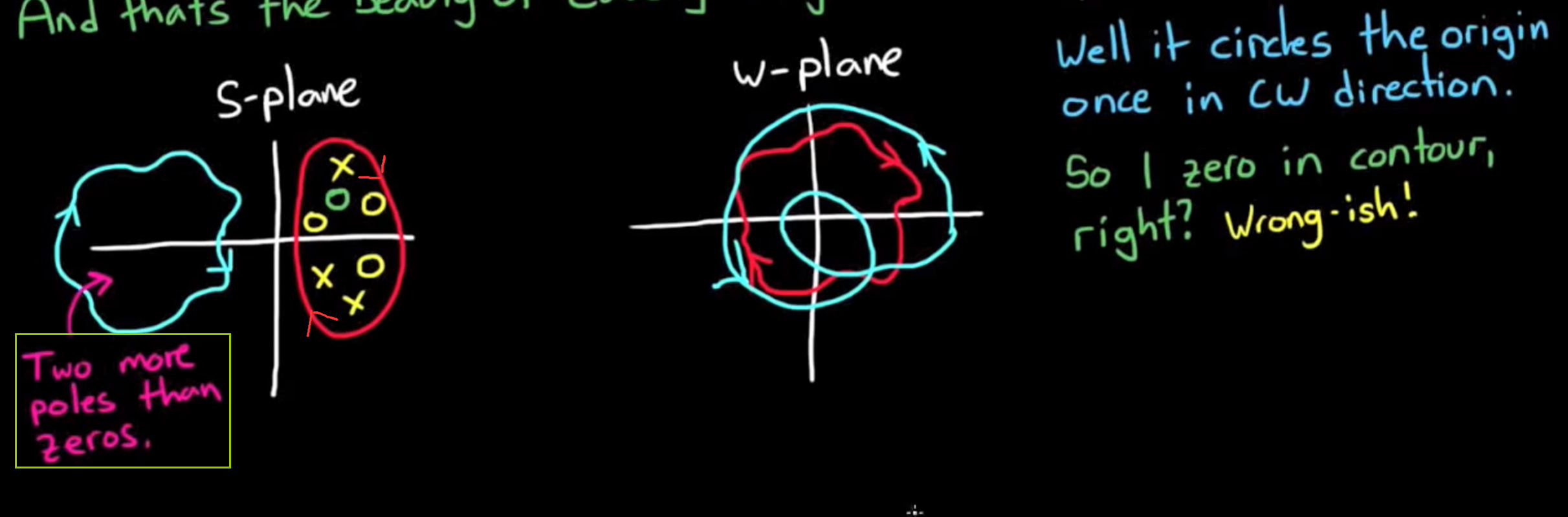
5. 根据以上论述, 柯西幅角原理能够帮助我们通过w平面上的映射曲线绕过原点的情况,推断出s平面中闭合曲线中存在的零点和极点的数量差. 注意是数量差, 要想知道具体的零极点的数量, 我们需要其它信息. 但是如果我们能设计好s平面中选取的闭合曲线, 就能用映射关系探究零极点在某一区域的大致数量, 这就是Nyquist稳定准则的思想. 这种特殊设计的曲线叫做Nyquist曲线, 用这种曲线映射画出的图就叫做Nyquist图.

Nyquist曲线, Nyquist图

1. Nyquist曲线是一个特殊设计的s平面上的闭合曲线, 如下:

   

    Nyquist曲线在w平面上的映射就是Nyquist图. 可以看到Nyquist曲线包含了整个右半区, 从原点出发沿jw正方向到无穷远, 在无穷远处环绕180°, 从jw负方向无穷远处会到原点. 所以我们通过Nyquist图环绕原点的次数和方向, 就可以知道系统在右半区零点和极点的数量差.

2. 由前面的介绍和演示可以知道, 开环系统Nyquist图向左平移1, 就是闭环系统Nyquist图, 那么我们可以不用画闭环系统的Nyquist图, 而是直接参考开环系统Nyquist图, 看看曲线围绕 (-1, 0j) 这个点的情况就可以达到同样的效果.

3. 用开环Nyquist图判断闭环稳定性的步骤:

4. 1. 画出开环Nyquist图
5. 2. 考虑曲线环绕 -1 这个点的情况
6. 3. 得出右半区零点极点数量差

手绘Nyquist图

真分传递函数

• 开始前先记住一个概念: 分子的阶数低于分母的阶数的传递函数, 称为严格真分传递函数 strictly proper; 分子阶数和分母阶数相等, 称为真分传递函数 proper; 分子阶数高于分母阶数, 称为 not proper. not proper的传递函数在现实中是不存在的.

分步手绘Nyquist图

• 传统的Nyquist绘制, 只需要将Nyquist曲线中每一个点映射到w平面上, 就完成了, 但是这样的机械式计算可能会导致对Nyquist曲线和Nyquist图之间的联系缺乏直觉上的感受. 所以我们选择将Nyquist曲线拆分成两部分分别映射, 并且只计算关键点的映射, 再根据一定规则连点成线, 即可手绘大致的Nyquist图.

• Nyquist曲线可以分为两部分, 落在虚轴上的部分和无穷远的部分:

   

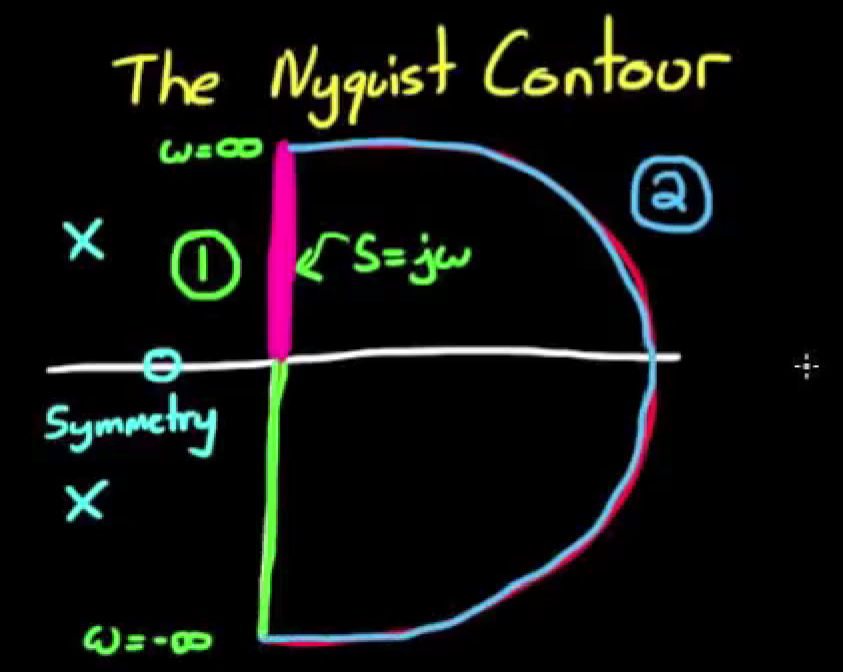
    1) 对于虚轴的部分, 我们需要将s = jω代入系统函数来完成映射, 由于虚轴的对称性, jω轴两边映射的图像是关于实轴对称的, 我们只需要计算ω从0到正无穷的部分;

    2) 对于无穷远的部分, 我们最后会发现在真分传递函数中, 无穷远的部分会被映射为同一个点.

       

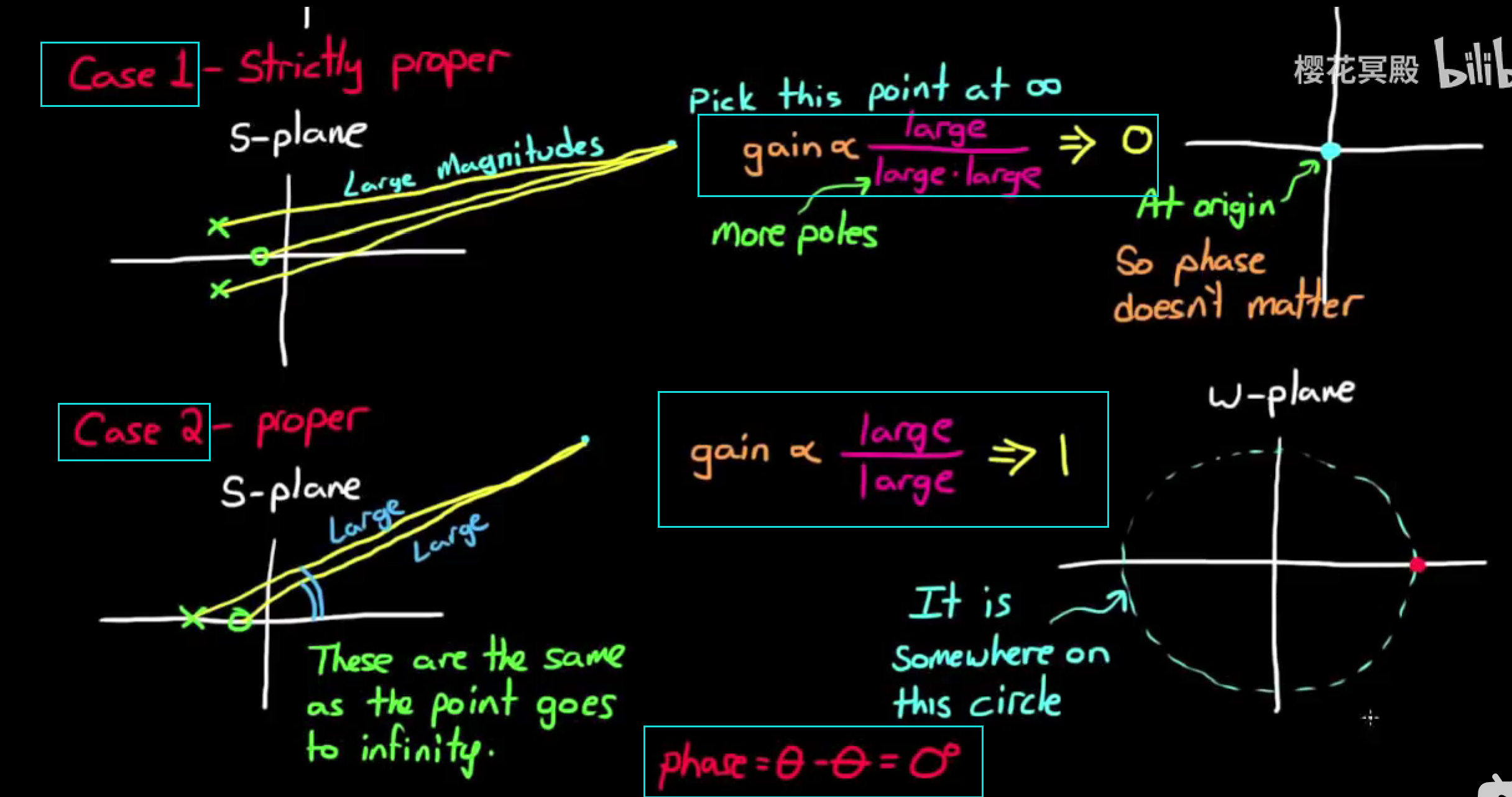
        由上图, 严格真分传递函数带入无穷远处的点, 增益为 ∞ / (∞*∞) = 0, 由于增益为0, 相位无关紧要, 对应点为原点;

        真分传递函数带入无穷远处的点, 增益为 ∞ / ∞ = 1, 而零点和极点的相位在极限状态下相等, 所以抵消, 相位为0, 对应点为 (1, 0j).

• 正常的画法应该是将s = jω带入传递函数, 然后将ω从0到正无穷扫描, 但是对于简单的传递函数, 我们完全可以用简单的方法估计出图像的大致形状, 方法如下:

    1) 找出ω = 0的映射点, 作为起点

    2) 找出ω = 无穷的映射点, 作为中点(一半曲线的终点)

    3) 找出Nyquist曲线与虚轴的交点

    4) 找出Nyquist曲线与实轴的交点

    5) 从起点出发, 穿过实轴, 穿过虚轴, 到达中点

    6) 从中点出发绘制对称图像

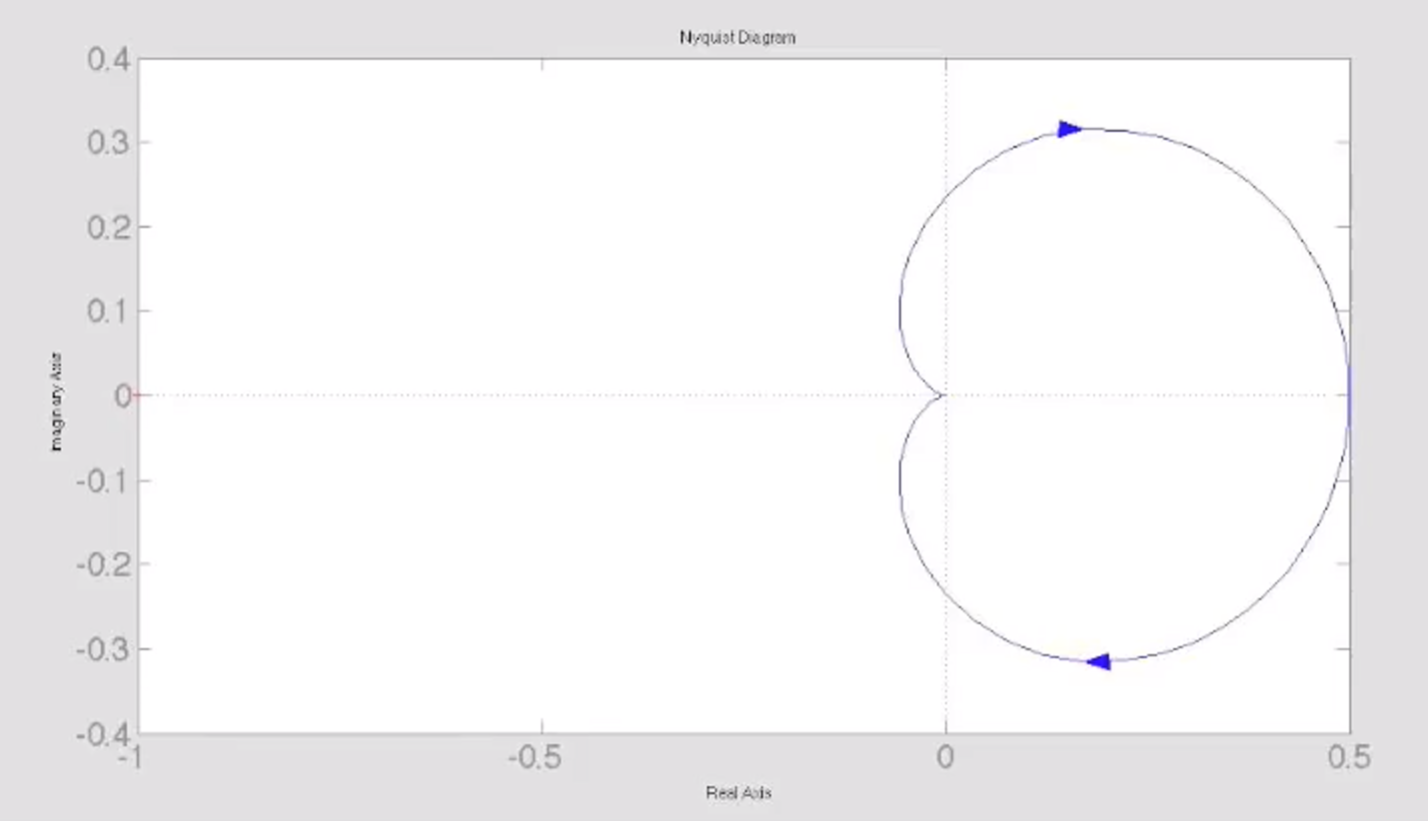
    - 以下是一个实例

       

        右上角为画出的Nyquist图, 红色轨迹和黄色轨迹均为可能的图, 但是不影响我们判断闭环系统是稳定的. 实际Nyquist图如下:

       

特殊情况: 虚轴上有一个开环极点

• 当虚轴上有一个开环极点, 我们绘制Nyquist图的时候, ω扫描到这个频率, 增益毫无疑问是无穷大, 但是相位无法计算. 根据柯西幅角原理, 计算这个映射点的相位需要知道从极点指向被选取点的矢量的相位, 然而这种情况下, 被选取点与极点重合, 根本没法说相位是多少. 这种情况不利于我们画Nyquist图.

• 解决方法很巧妙, 假设那个开环极点就在原点处, 那么我们稍微改变Nyquist曲线, 让曲线从右边绕过原点, 但是间隔很小, 以至于我们不会漏掉任何原点附近的右半区开环极点, 也就是说如果存在这样的额外极点, 那就从它们当中绕过去, 只排除原点处的极点, 如下图:

   

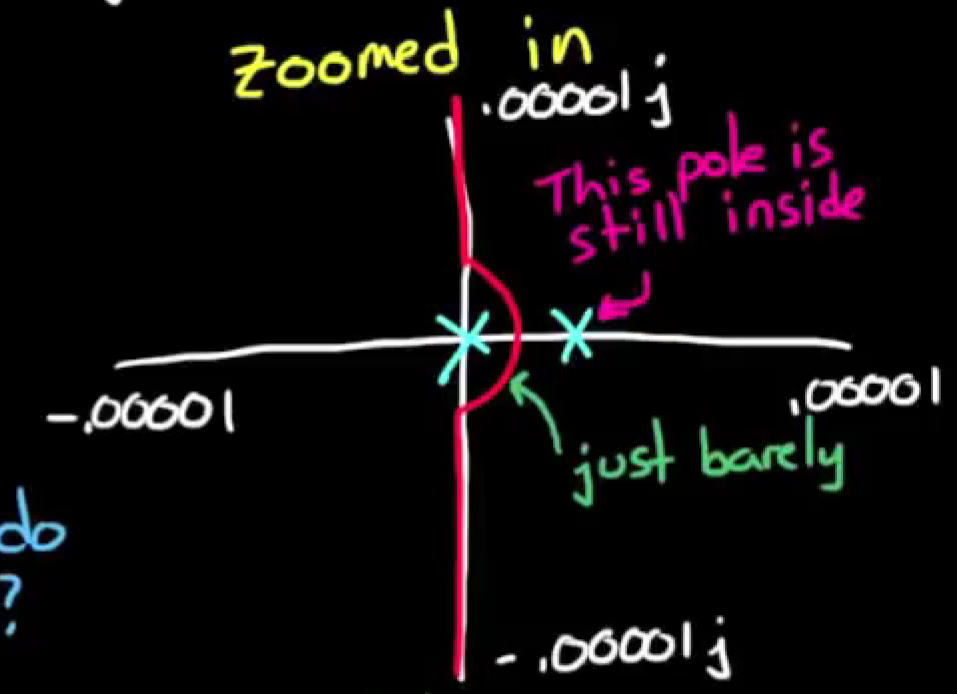
    然后用修改过的Nyquist曲线映射出Nyquist图. 这样的Nyquist图会有延伸向无穷的部分, 但是大体上还是能看出其环绕 -1 的情况. 大概像这样:

   

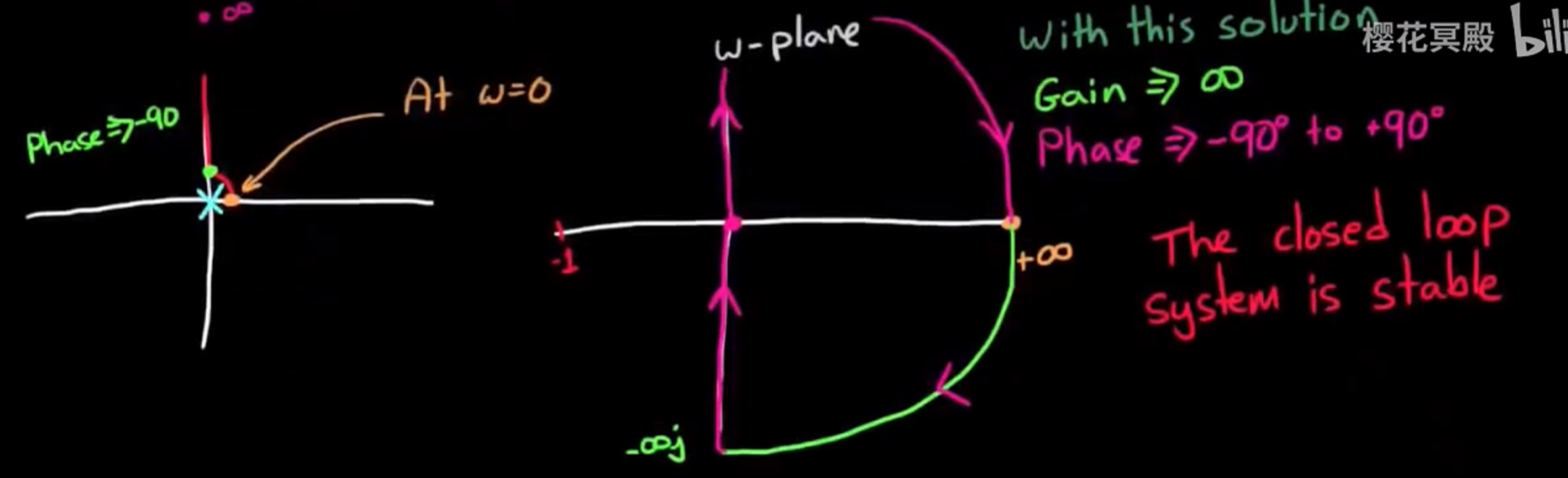
    当然, 改变Nyquist曲线的方法也可以是稍微向左绕过原点处的极点, 即将这一极点包含进曲线中, 如图:

   

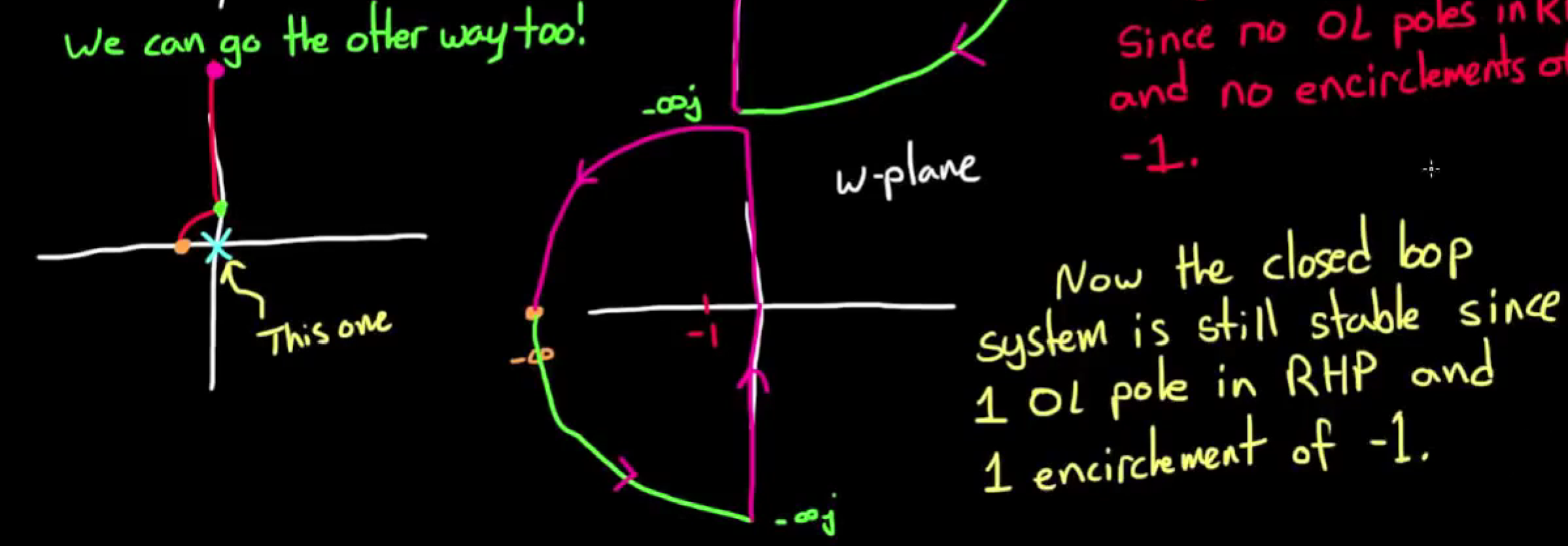
    由于我们已经知道Nyquist曲线中一定有一个极点, 根据曲线环绕 -1 的情况, 还是能做判断.

• 虚轴上存在开环零点呢? 不必理会, 因为ω扫描到开环零点时, 增益为0, 虽然相位仍然不确定, 但是一个从原点出发的矢量幅度为0, 自然不用关心其相位.

再次提及Nyquist判据的好处

• 系统函数十分复杂时, bode plot可能无法直观看出系统稳定性, 因为有太多的极点和零点在影响bode plot的形状. 这时画出Nyquist图, 可以轻松看出系统稳定性特点, 例如这个例子:

    - TF:

       

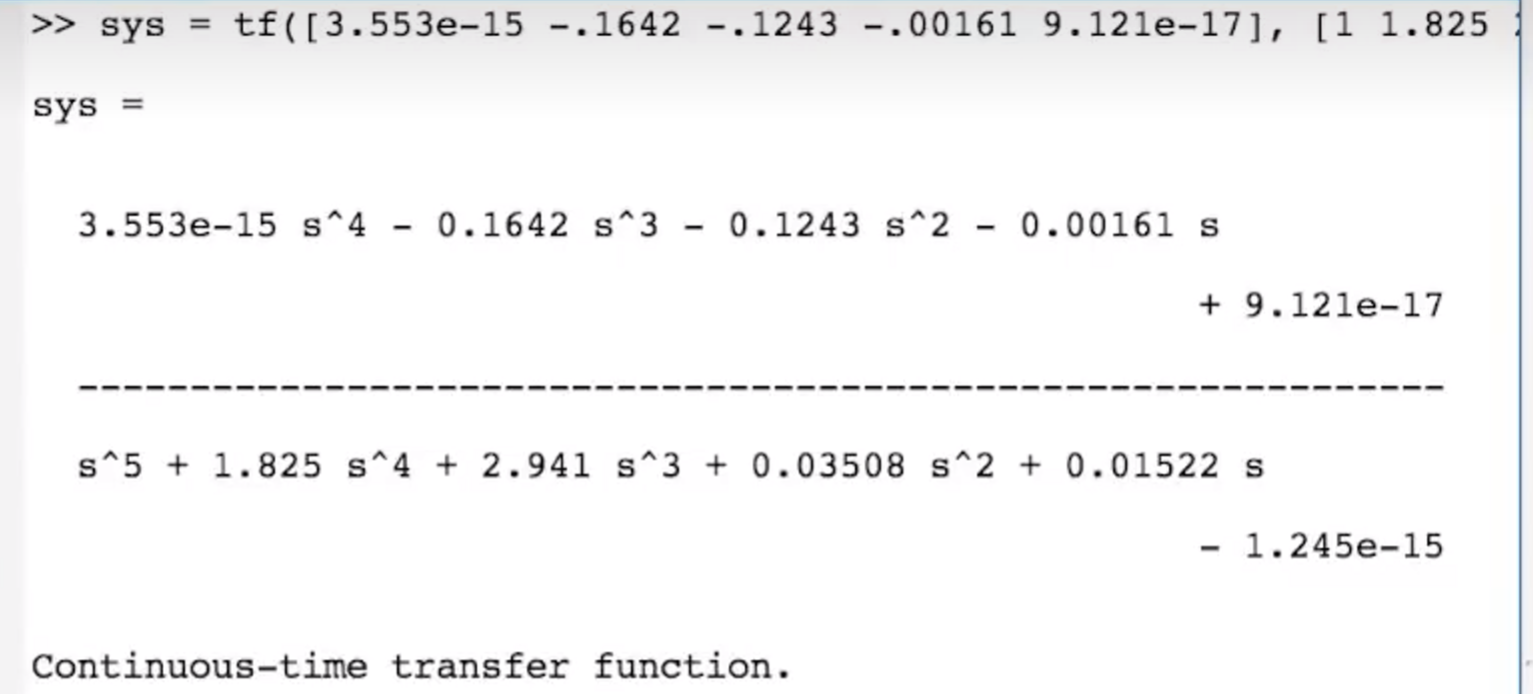
    - bode plot:

       

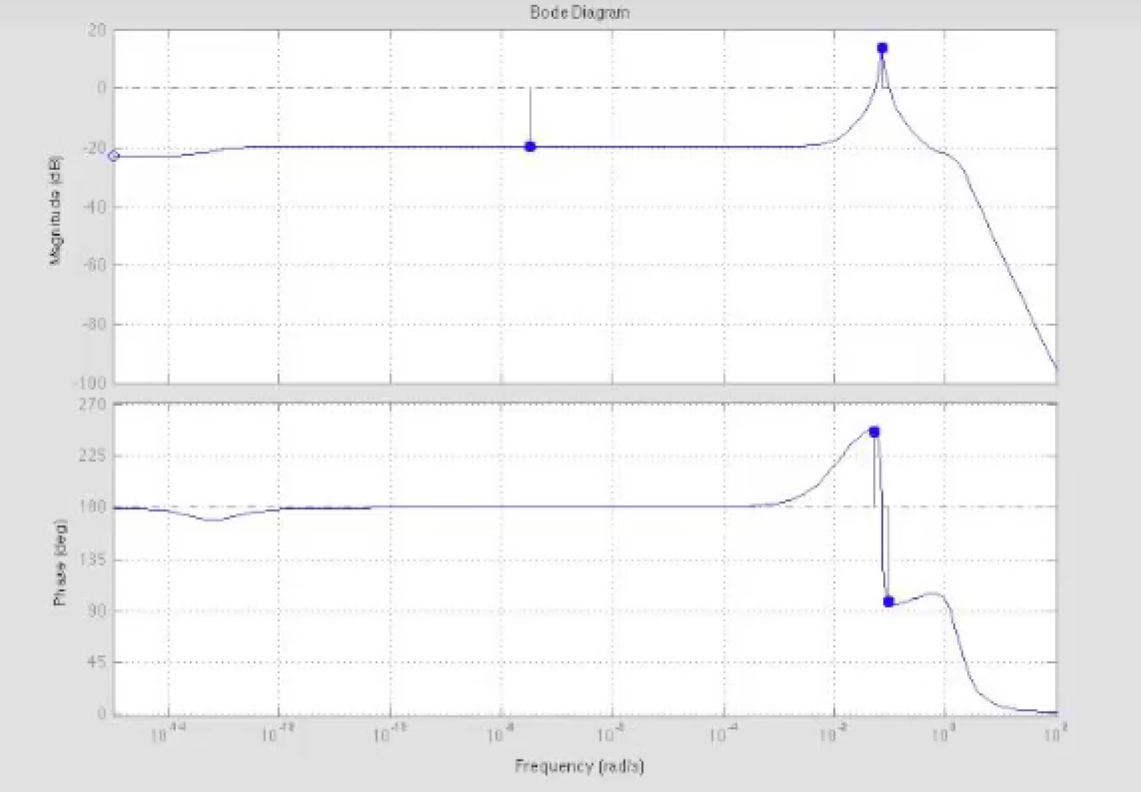
    - Nyquist plot:

       

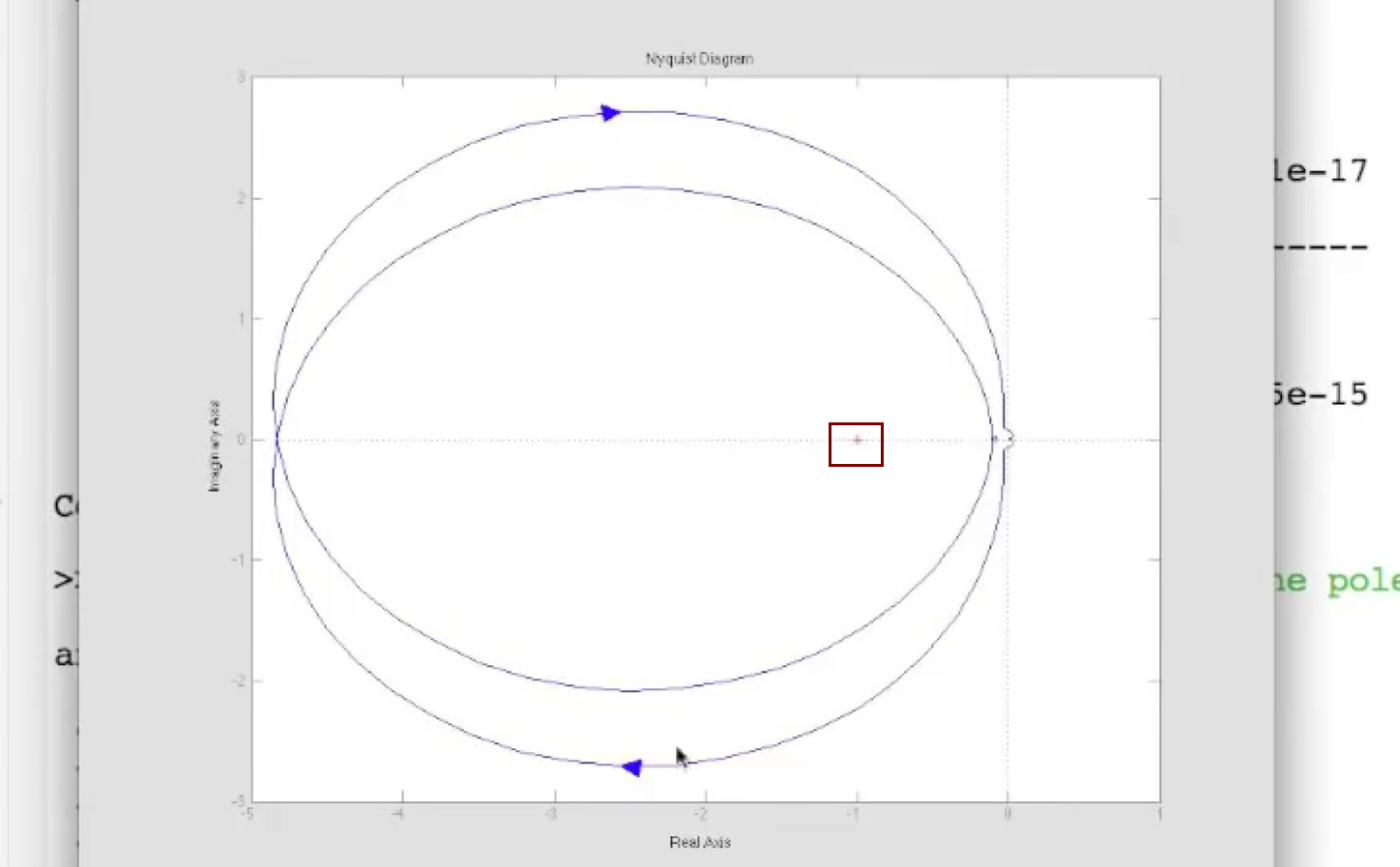
    - bode plot看半天, 不如Nyquist plot绕两圈搞定.