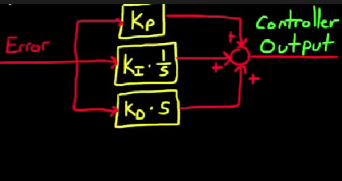
什么是PID控制器
- P I D, 代表比例 积分 微分, 本人对PID已经比较熟悉, 不做过多基础知识的记录

三个项分别对误差进行比例, 微分, 积分处理, 然后相加得到输出量
- 一般来说,PID控制器接在实际执行器的前端,输入PID控制器的是执行器实际输出与期望输出之间的差值,产生的是下一步执行器的输入量. PID脱离执行器(被控制的系统)没啥意义, PID存在的意义是给予本来需要手动控制的系统自动控制的能力.
用实际题目结合PID与根轨迹
- 有一个柴油发动机, 输入柴油使转轴旋转, 输入阀门角度与输出转速之间关系如下:

给它加一个PID控制器实现自动控制, 要求阻尼比不小于0.7, PID控制器的传递函数已经给出, Kp和Kd已经确认:
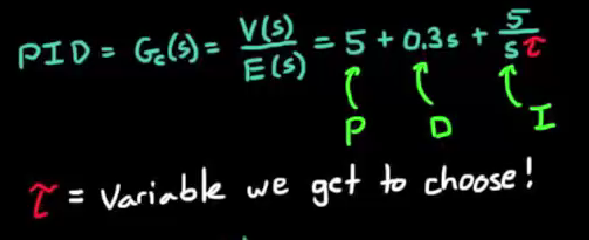
题目要求:
1) 画出根轨迹图, 即闭环控制系统特征方程的根随t变化的变化
2) 确认t值, 确保大于0.7的阻尼比
3) 确认最终系统的极点
- 画出根轨迹, 先画出系统框图:
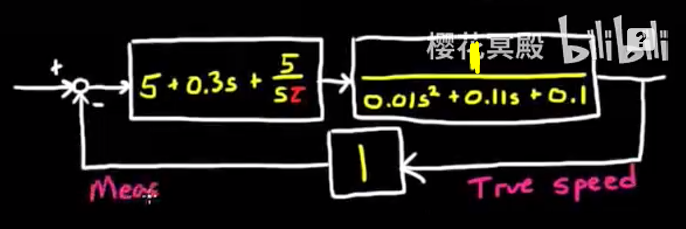
这里的反馈选择真实反馈, 即输出转速不加增益地与输入转速比较. 这里增益给多少取决于需求, 类似于想要更快的响应就给误差加一些倍数, 但是与比例控制还是不太一样.
想要画根轨迹图, 我们先将闭环系统函数写成以下标准形式:

其中, k * G(s) = PID系统函数 * 发动机系统函数, 即总开环系统传递函数. 现在我们要把散落在式子各处的 t 提出来, 作为未知参数 k, 同时也得到了关键的G(s) :

接下来画root locus就围绕着G(s), 首先观察到G(s)有三个零点, 没有极点, 在s平面上画出三个零点, 并根据手绘根轨迹规则画出根轨迹交汇点, 渐近线, 然后画出大致的根轨迹
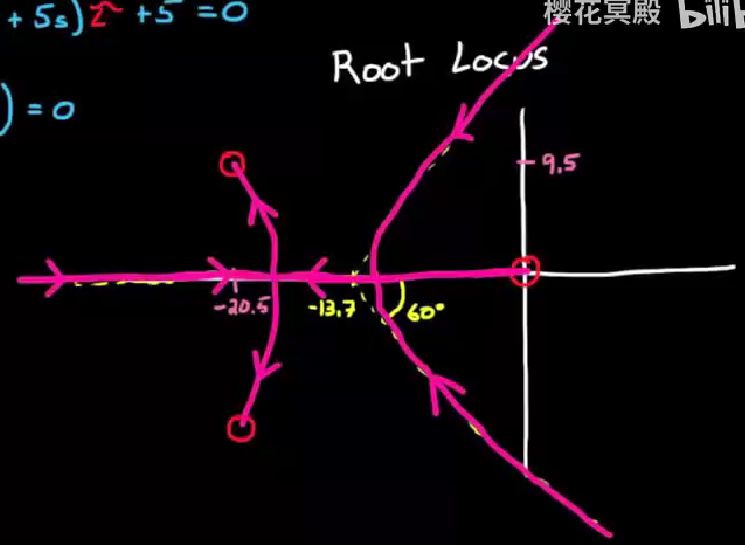
让我们观察这个根轨迹, 当t很小时, 一对共轭极点在右半区的无穷处, 此时系统不稳定; 随着t增大, 共轭极点移动到虚轴上, 达成临界稳定; t继续增大, 极点进入左半区, 系统变稳定; 继续增大, 阻尼比也增大, 所有极点来到实轴上时, 系统阻尼; t继续增大, 共轭极点又会离开实轴, 系统又表现出震荡.
- 由于题目要求0.7的阻尼比, 大概对应直线在45°左右, 因为cos(45°) ≈ 0.707. 显然目标阻尼比的直线不会穿过下图中蓝色区域:
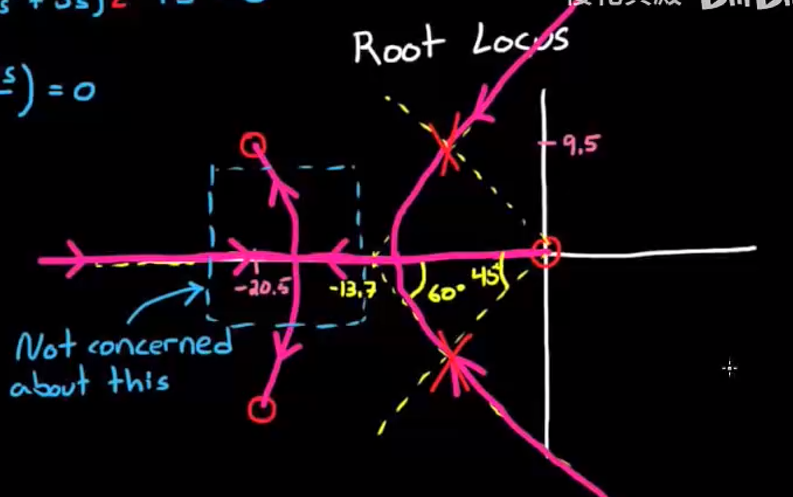
所以蓝色区域手绘根轨迹是否准确无关紧要, 重要的是阻尼比直线与根轨迹相交的部分.
现在我们知道阻尼比直线, 又知道直线与根轨迹在渐近线附近相交, 则为了估计交点的位置, 这里我们直接采取直线与渐近线的交点作为近似极点位置, 这个极点很有可能满足我们对于阻尼比ζ >= 0.7的要求. 最后解得极点在 (8.7, ±8.7j)附近:

将这个点代入特征方程, 解出t的取值, 此时t可能会有虚数成分, 这是因为一切数值都是估计, 正常的计算结果是不会有虚部的, 这里直接舍弃虚部取实部
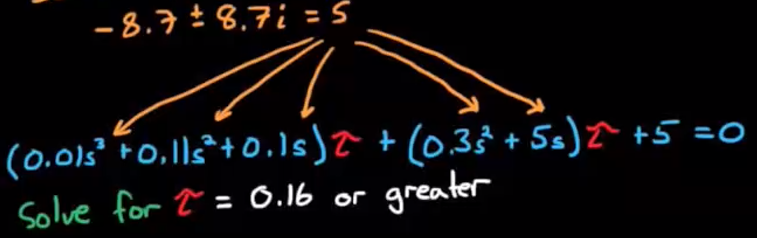
- 经过计算, 我们已经得到了两个极点的位置(8.7, ±8.7j), 要想得到第三个极点的位置, 只需要运用手绘根轨迹中讲过的rule 9: 如果有两个以上指向无穷的根轨迹, 那么在根移动的时候, 所有根的实坐标相加是一个常数.

- 最后用matlab验证计算是否正确.
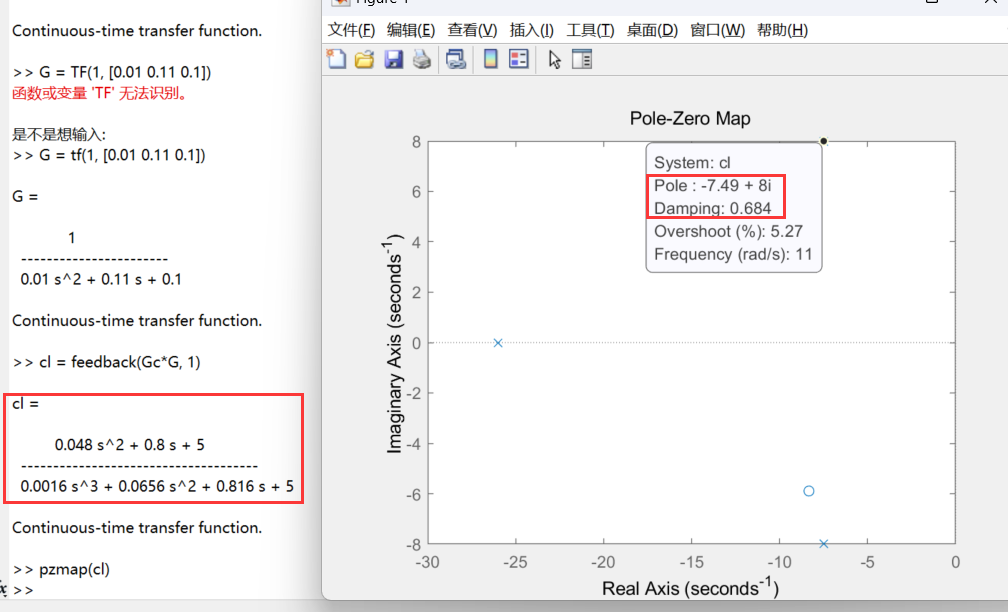
最后得出的极点阻尼比接近0.7, 说明t取0.16在计算上没什么问题