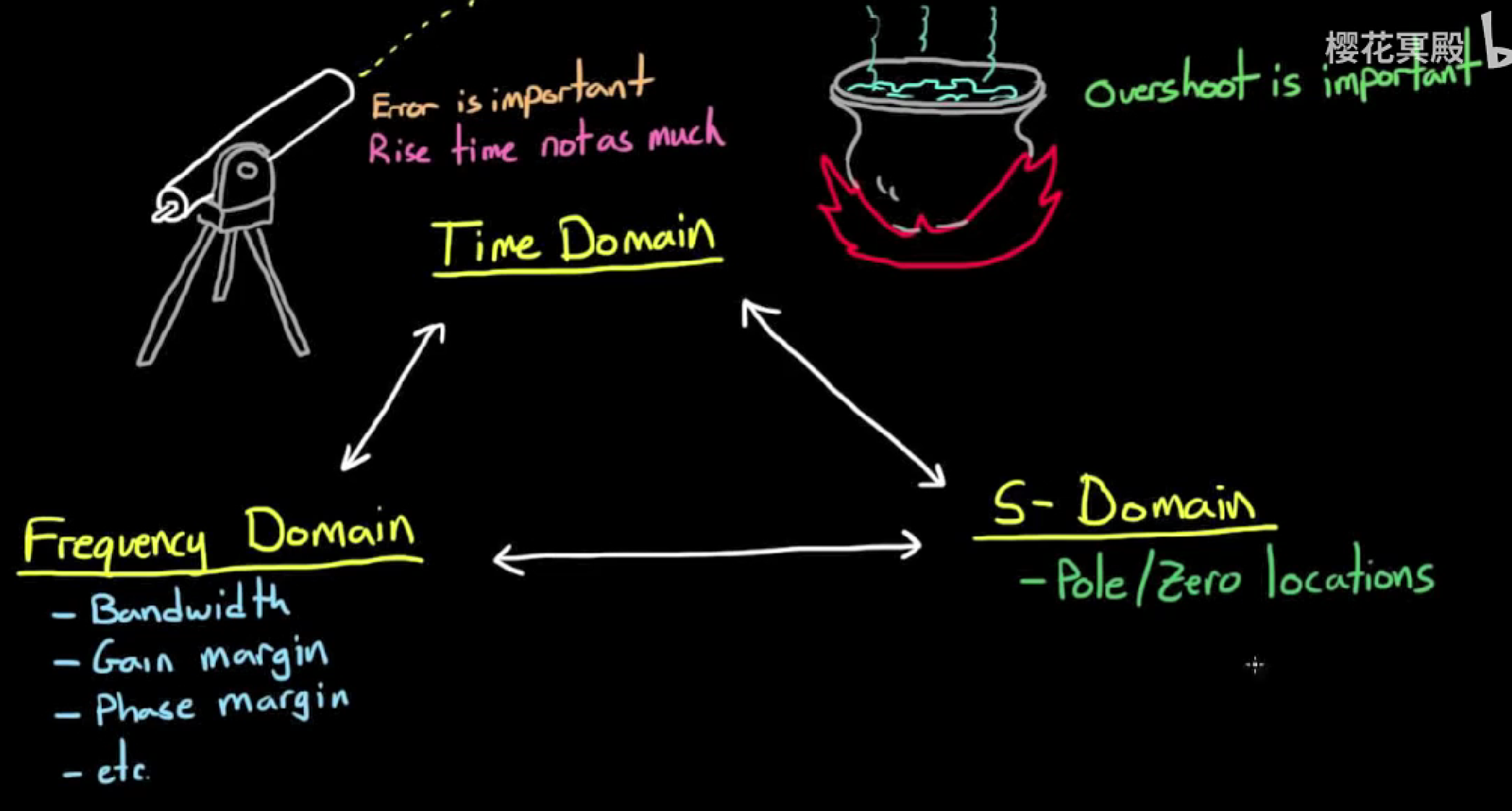
强调二阶系统, 以及二阶系统中阻尼比 ζ damping ratio 的重要性
首先需要说明的是, 只有二阶系统或类二阶系统才有阻尼比这个概念
二阶系统在现实中很常见, 例如弹簧-质量-阻尼, RLC电路, 这些系统具有不同的物理性质, 但是其特征方程都可以用阻尼比ζ和固有频率ω来描述, 如下:
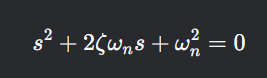
例如弹簧-质量-阻尼系统在时域的动态方程可以这样写:
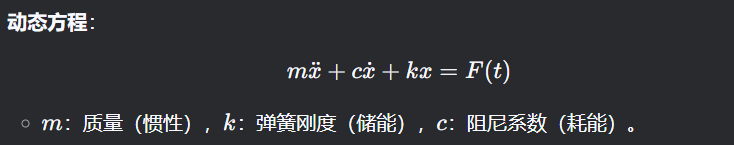
Laplace变换后, 对方程标准化, 可以得到如下特征方程:
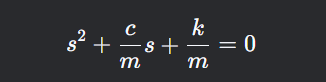
特征方程系数可以拆解为阻尼比和固有频率, 如下:
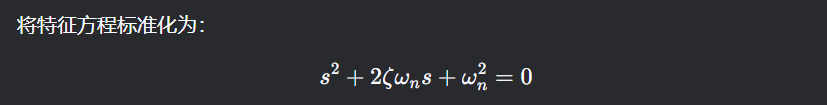

这样就实现了用两个关键参数来描述系统. 对于其它二阶系统也是同样的操作方法, 最后得到的阻尼比和固有频率, 不仅是数学上的推理, 还能表征系统响应的一些关键特征, 例如弹簧-质量-阻尼系统中系统受到脉冲激励, 那么弹簧震荡的频率和衰减速度就可以从这两个参数中得到.
- 常见的二阶系统主要特征是存在两个储能器和一个耗能器, 例如RLC系统中, LC组成类似两个储能器之间交换能量的振荡结构, R是耗能器, 导致能量衰减.

- 二阶系统为什么重要? 我们为什么偏爱二阶系统?
- 二阶系统是建立其它高阶系统的基础
- 很多高阶系统通过主导极点实际上表现出二阶系统的特征
- 不同的物理性质可以用阻尼比和固有频率统一描述, 具有通用性
- 设计便捷, 这点我有发言权, PD控制器很好调, 套公式做题即可😋
- 再说一点, 我们熟悉的s平面上的极点除了用直角坐标直接表示, 还可以用极坐标来表示, 而极坐标的两个参数就是阻尼比(对应着角度)和固有频率(对应着模长), 如下图:
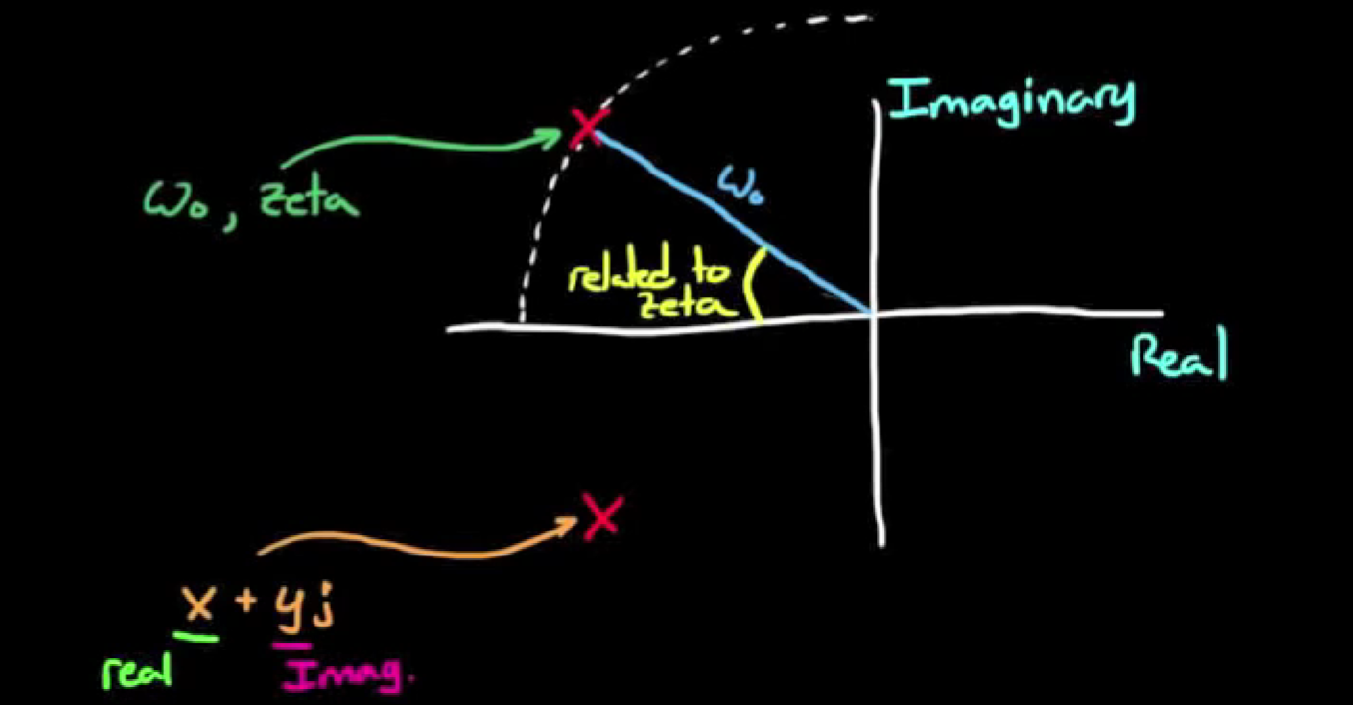
ζ -> zeta, 而且前文提到过, 阻尼比是极点与原点连线的锐角夹角的余弦值.
阻尼比和固有频率决定了极点的位置, 反过来说, 通过设计极点的位置, 我们也能赋予一个系统特定的阻尼比和固有频率. 这是一个我们通过设计极点位置来影响系统性能的实际例子.
如何描述系统的性能? 我们为什么要在s域调整系统的性能?
- 对于一个二阶系统的阶跃响应, 有很多术语可以用来描述, 例如上升时间, 峰值时间, 稳定时间, 超调量, 稳态误差, 如图:
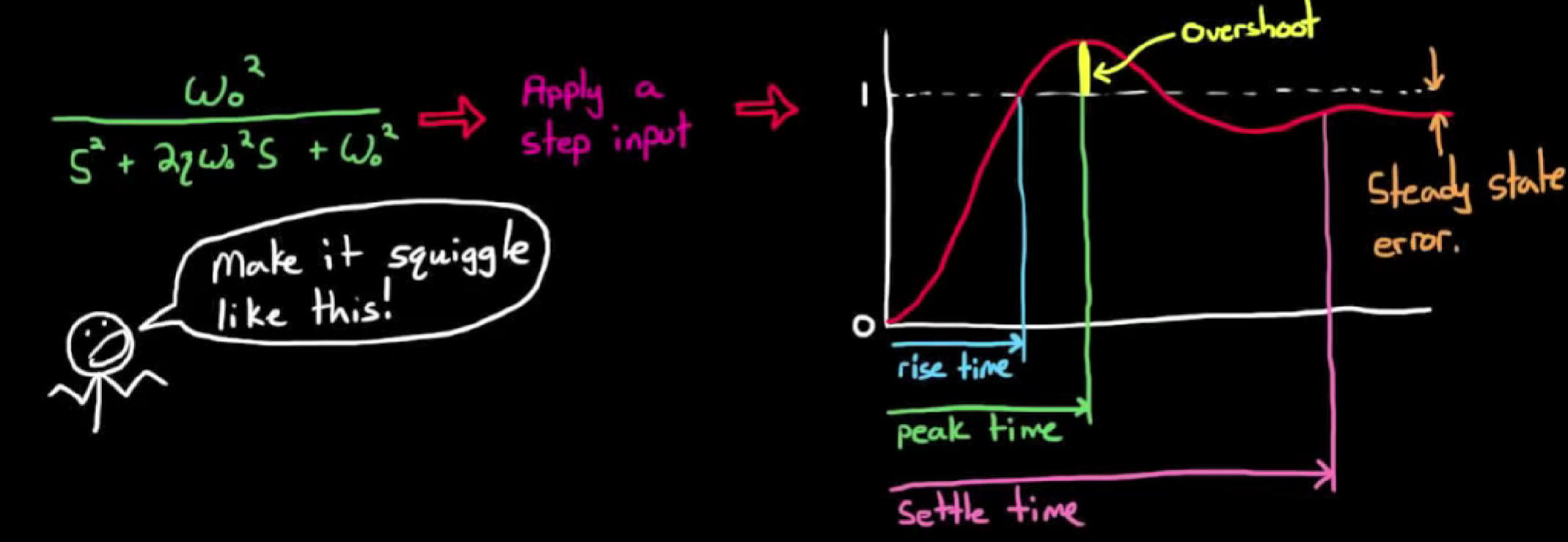
注意到这些描述是在时域上进行的, 也就是说, 当我们对这些指标有要求, 都是时域上的要求. 我们还可以在频域上分析系统, 频域上的指标有带宽, 增益裕度, 相位裕度等.
对一个系统的需求, 最终是在时域上体现的, 但是我们目前为止学到的方法都是在s域上对系统进行分析和设计的, 时域上没有类似的方法. 那么为了利用s域上的这些方法, 我们需要知道如何将时域的需求转化为s域的需求, 否则每次在s域上设计系统后, 都需要转换回时域看结果, 效率十分低下.
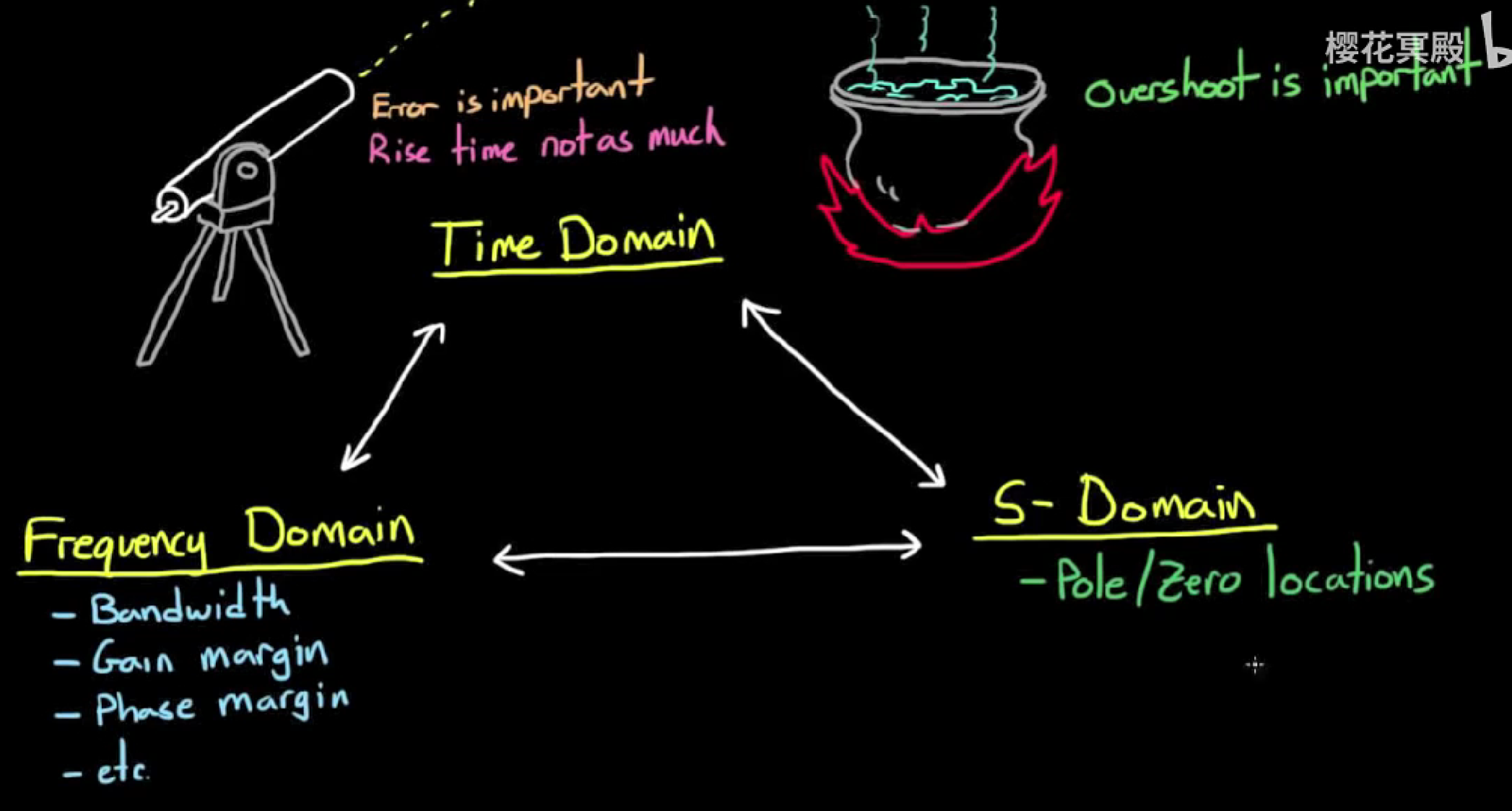
这种需求转化, 具体说就是将时域需求转化为s域上系统零点和极点的目标位置.
- 一个例子是, 视频观众的提问: 我们对一个系统有阻尼比的要求, 要求系统阻尼比刚好能造成15%的超调量, 如何获得阻尼比?
- 让我们首先把题目补充完整. 鉴于目标是获得阻尼比的值, 那么有一个前提是: 这个系统是一个二阶系统, 因为只有二阶系统或者表现为二阶系统的系统, 才有阻尼比这个概念. 我们不能只说这个系统有多少的阻尼比, 而不知道这个系统是一个二阶系统. 这个错误提醒我们定义任何事情都是有前提的, 否则就是在胡扯.
- 在二阶系统中, 存在一个公式可以将超调量转化为阻尼比, 如下:
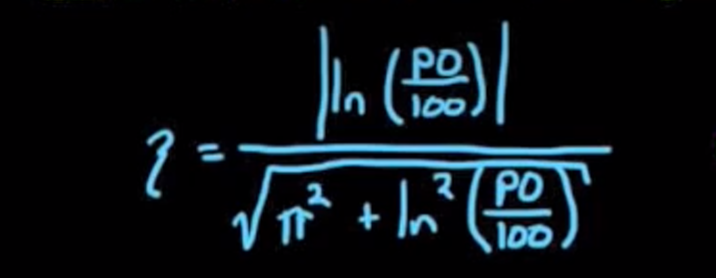
还是之前的问题, 注意我们只能在二阶系统中使用这个公式, 如果在更高阶的系统中想做类似的转换, 需要查清楚对应的公式.
- 在matlab中实现, 定义超调量, 计算阻尼比, 建立传递函数, 然后输入阶跃响应并画图, 看看我们的计算是否正确.
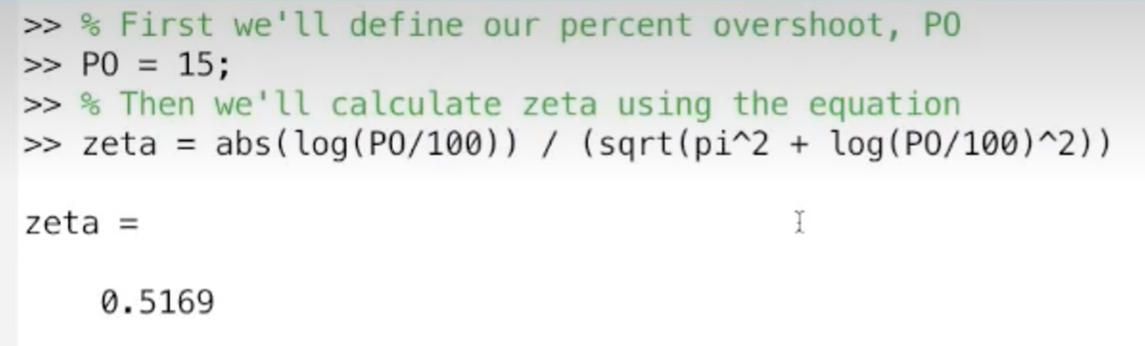
建立传递函数, 不能只用阻尼比, 还需要固定频率, 这里先给出结论: 固定频率不影响超调量, 所以随意给一个值
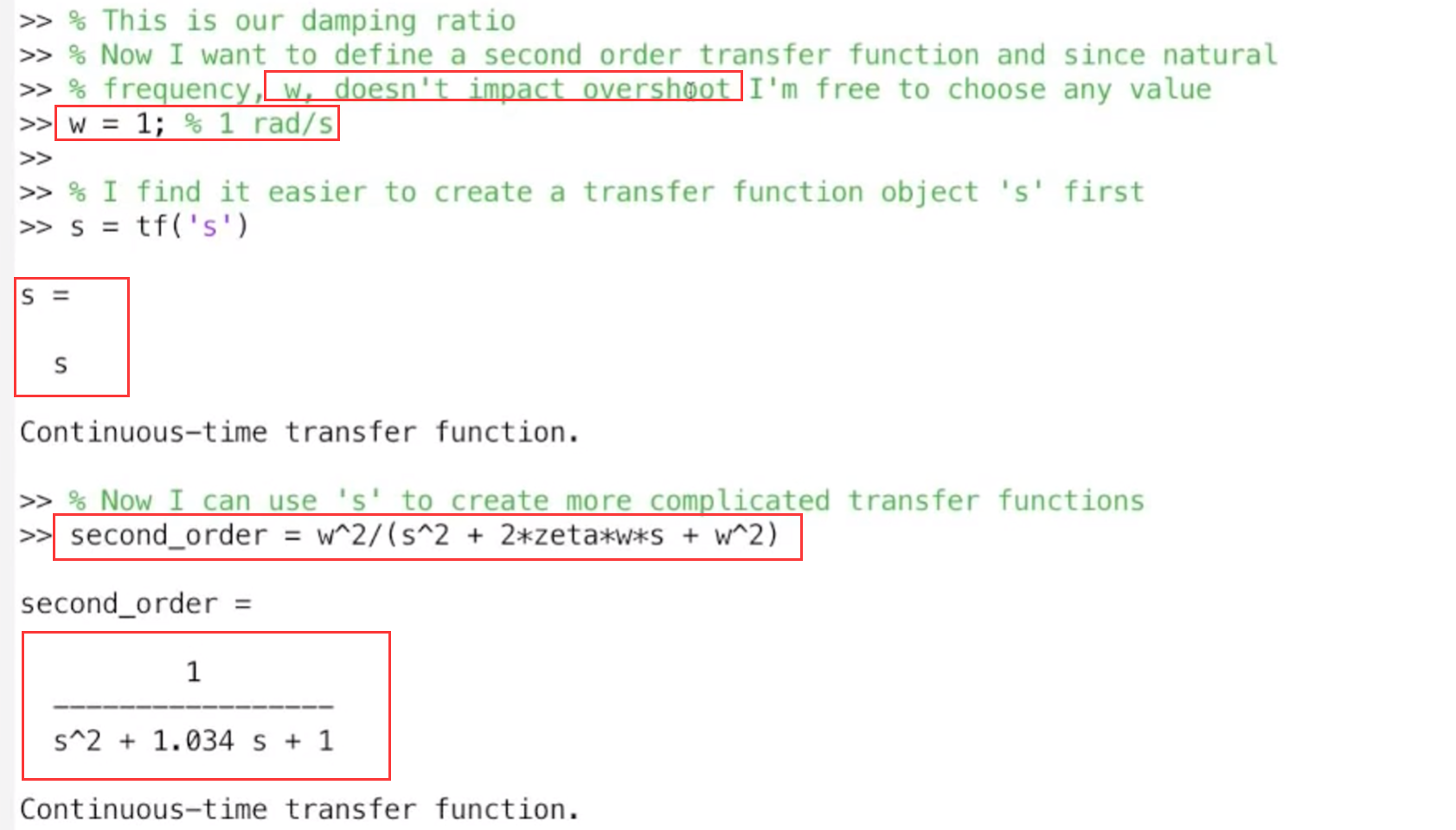
输入阶跃信号得到阶跃响应
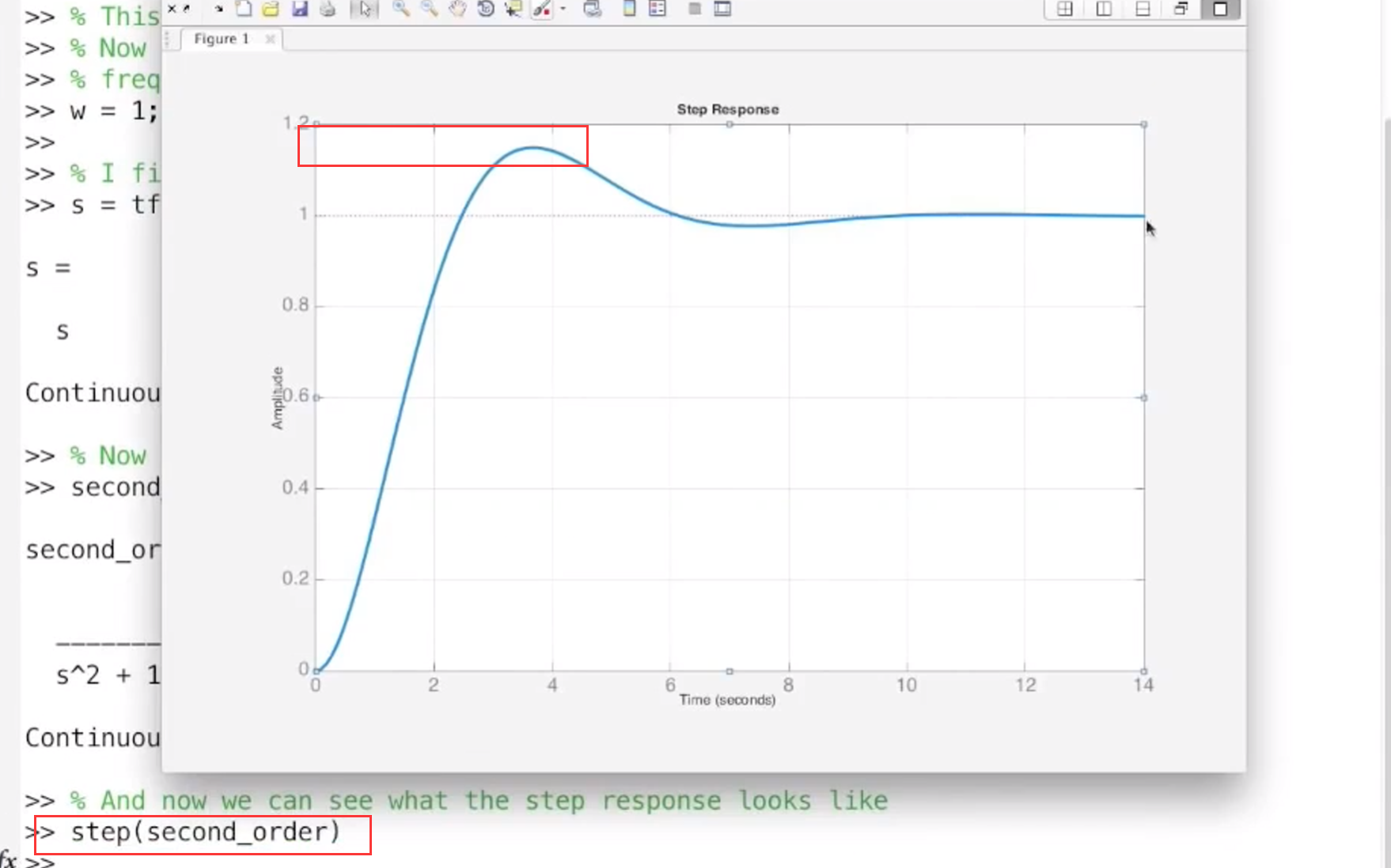
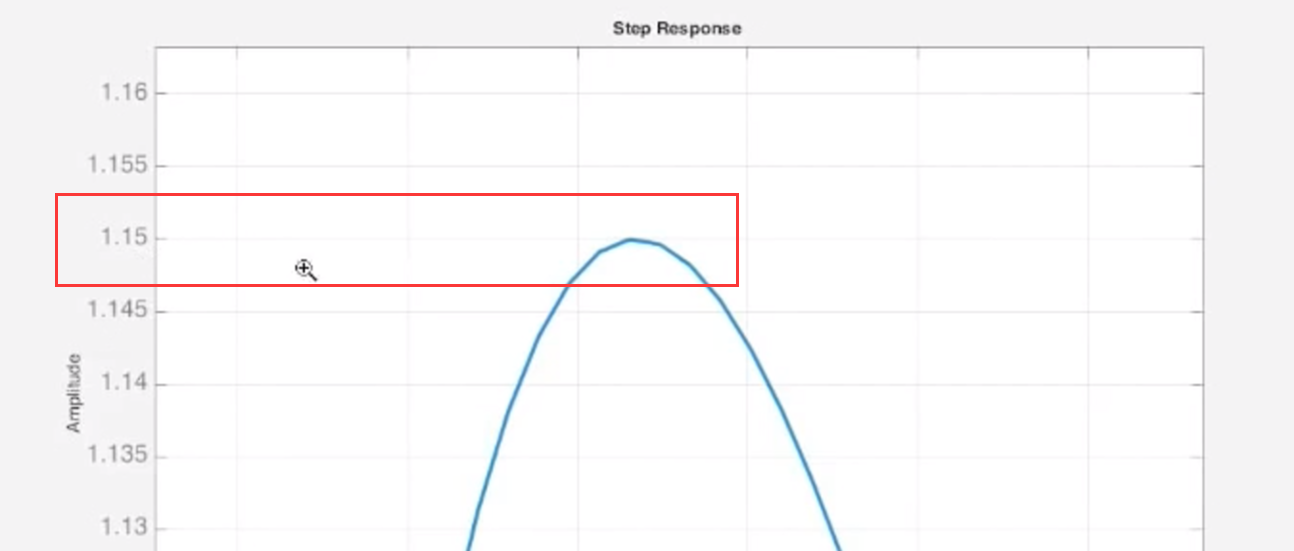
可见超调量精确控制在15%
- 为了验证之前的结论: 固有频率不影响超调量. 在matlab中给出一系列递增的固有频率而不改变阻尼比, 画图验证:

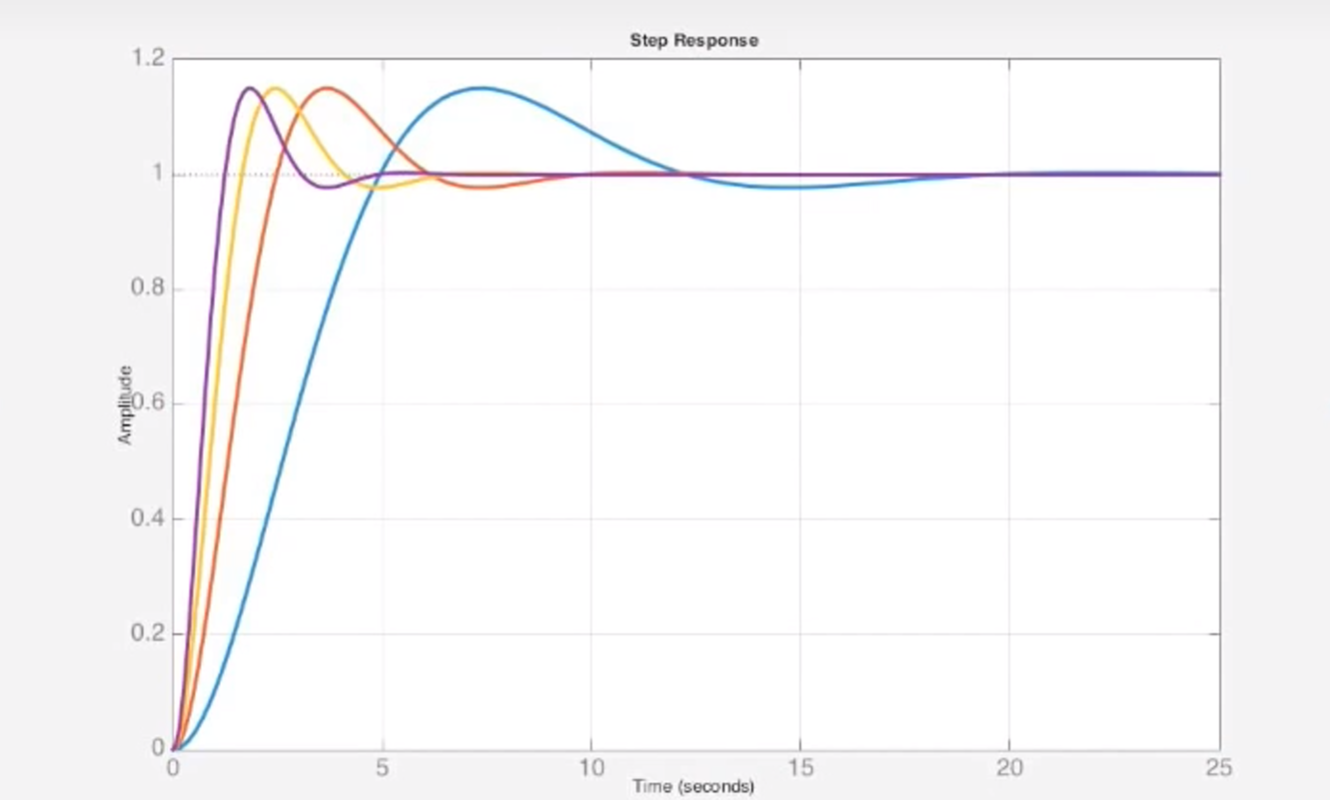
结论正确, 超调量一致, 只有上升时间和稳定时间受到影响.
让我们使用pzmap函数继续画出零极点图, 观察极点的移动:

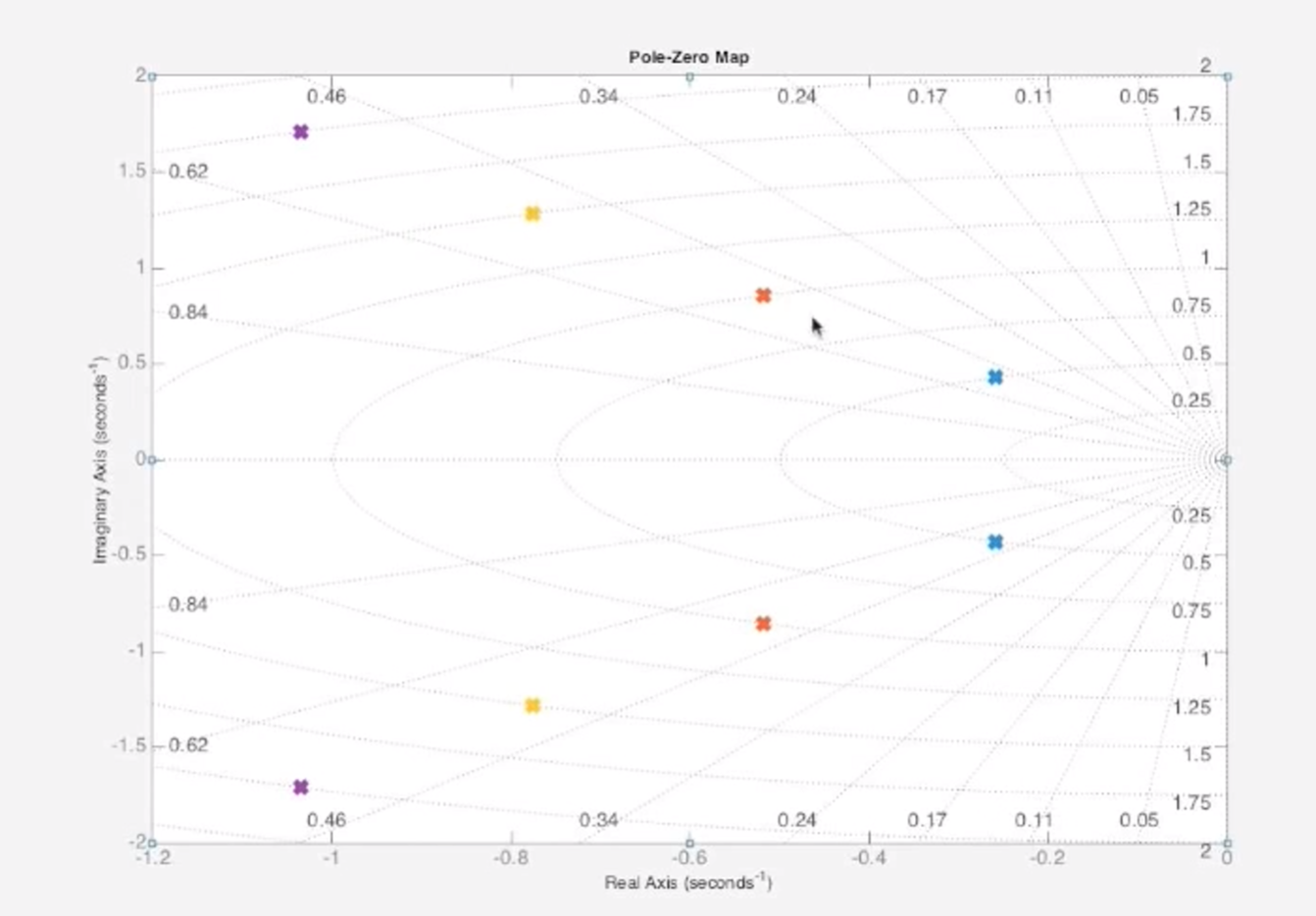
结果表现为一条过原点的直线, 与之前所述一致, 直线上所有极点有相同的阻尼比, 但是固有频率不同.
阻尼比ζ如何大于1?
之前说到ζ是直线夹角的余弦, 从单纯数学角度来看, ζ不可能大于1, 但是首先我们要知道, 现实世界中是存在过阻尼的系统的, 也就是ζ > 1的系统, 基于这一点, 我们的思考方式应该从”阻尼比能不能大于1?”转换为”阻尼比本来就能大于1, ζ = cos(β)的合理性如何?”.
实际上,在之前的介绍中我漏掉了一个关键的条件, 那就是当ζ < 1时, ζ = cos(β). 这好像是一句自圆其说的废话, 但是它并不是理所当然, 而是有严谨的数学论证的:
- 我们需要知道ζ = cos(β)怎么来的. 当ζ < 1时, 特征方程 s²+2*ζ*ω*s + ω² = 0 的解可以用二次方程根的公式表示如下:

化简完成后的表达式在紫色框中, 当我们假设ζ < 1时, 根号下的部分小于1, 这是一对共轭复数根, 在虚平面上表示如下:
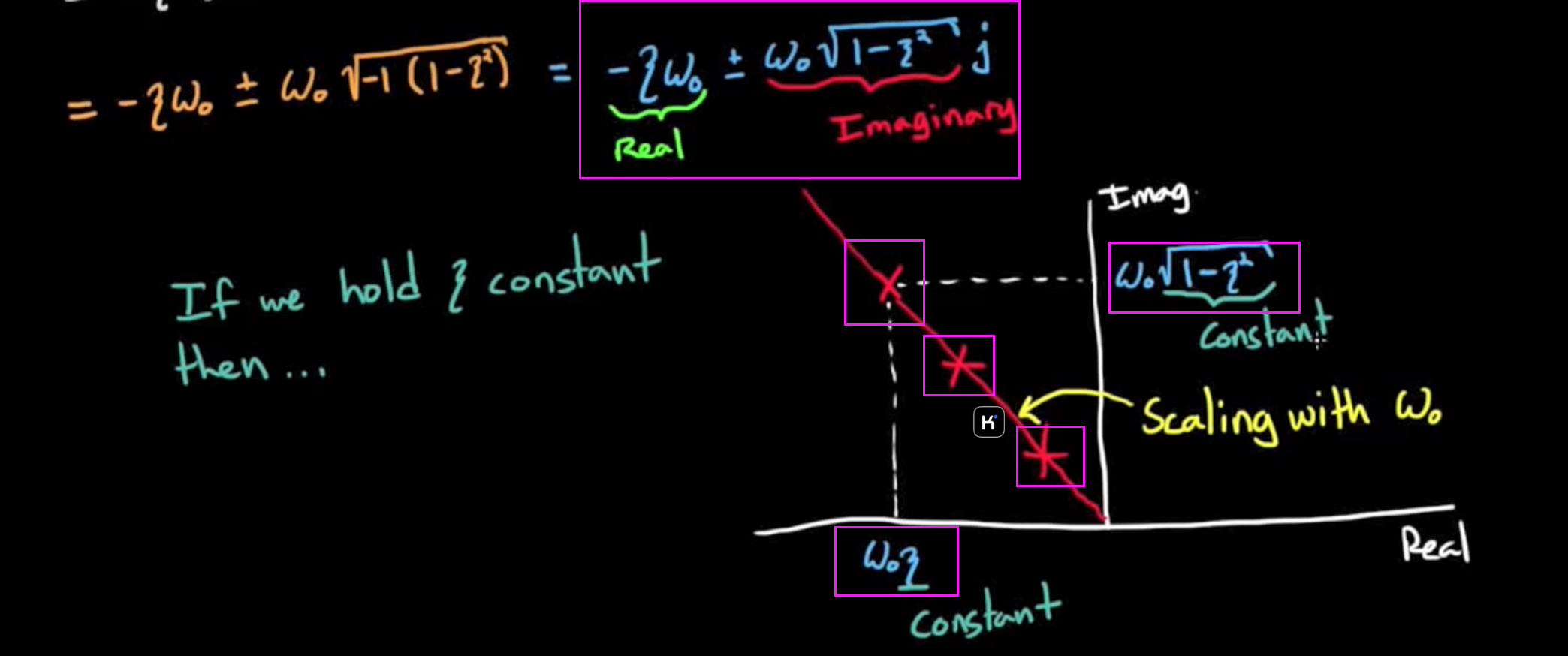
现在将根与原点连线, 这条直线与实轴夹角是多少? 鉴于我们知道实轴和虚轴坐标, 就能用三角函数知识, 得到直线长度为ω, 并将夹角的余弦值表达出来:
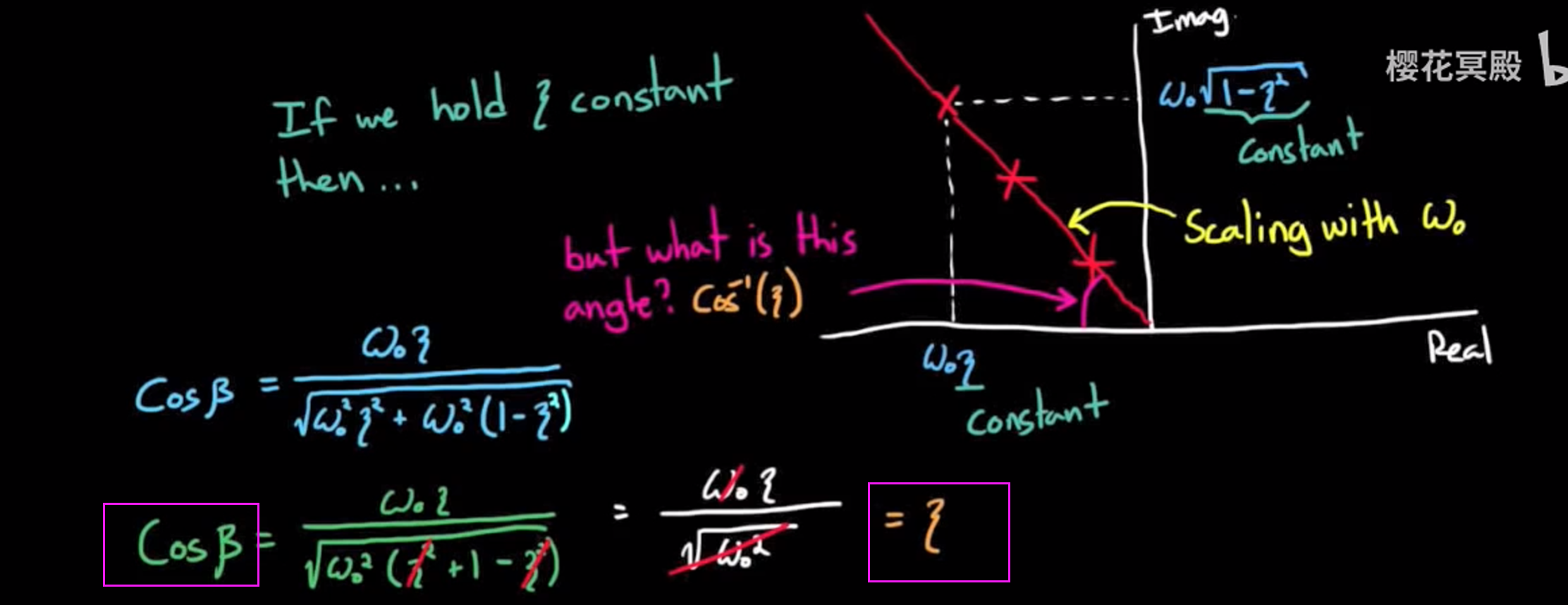
这就得到了我们熟悉的公式. 但是注意一系列的前提都是ζ < 1.
- 当ζ > 1时, 会怎样? 我们应该回到最初的二次方程根公式, 观察到如果ζ >= 1, 那么特征方程的根根本就没有虚部, 此时根在实轴上, 随着ζ变化而移动, 一个增大另一个减小. 此时回看cos(β), 无论ζ怎么改变, cos(β) = 1, 也就是说此时这个计算公式完全不适用了.
- 这个问题提醒我们, 任何公式在推出时, 都是带有前提的, 我们要搞清楚此时的情况是否满足前提, 再来利用公式计算, 而不是瞎套.