闭环系统的稳定裕度

为什么是闭环系统?

• 并不是一个系统从开环变为闭环都会带来稳定性的提升, 就像调PID一样, 过大的Kp, Ki, Kd会导致输出震荡, 发散, 不稳定. 也就是说, 闭环系统的各项参数影响着稳定性.
• 系统各项参数可能受很多条件影响, 例如温度, 控制器延迟, 器件磨损带来机械性能改变, 所以闭环系统存在稳定裕度这种指标, 用于描述系统承受这些变化而保持稳定的能力.

什么是稳定裕度?

• 稳定裕度由两方面组成, 增益裕度和相位裕度
      1) 增益就是单纯的对信号进行放缩;
      2) 相位是输入信号经过系统后, 系统给信号引入的相位移动
      3) 两者可以用bode图表示出来, 一般来说系统对不同频率成分的输入信号的增益和相位改变不同.
• 什么情况下会造成一个闭环系统不稳定?
      - 设开环系统为G(s), 闭环系统的特征方程为G(s) + 1 = 0, 即 G(s) = -1, 这个情况表现在bode图上, 就是系统对某一频率的增益既为0dB(10log(|-1|) = 0dB), 相位移动又为**-180°**(一个信号乘以-1, 本质上是增益为1然后翻转信号, 分解为正弦信号来看就是引入180°相位变化).
      - 如果一个系统的bode图出现了这样的情况, 就说明它不稳定.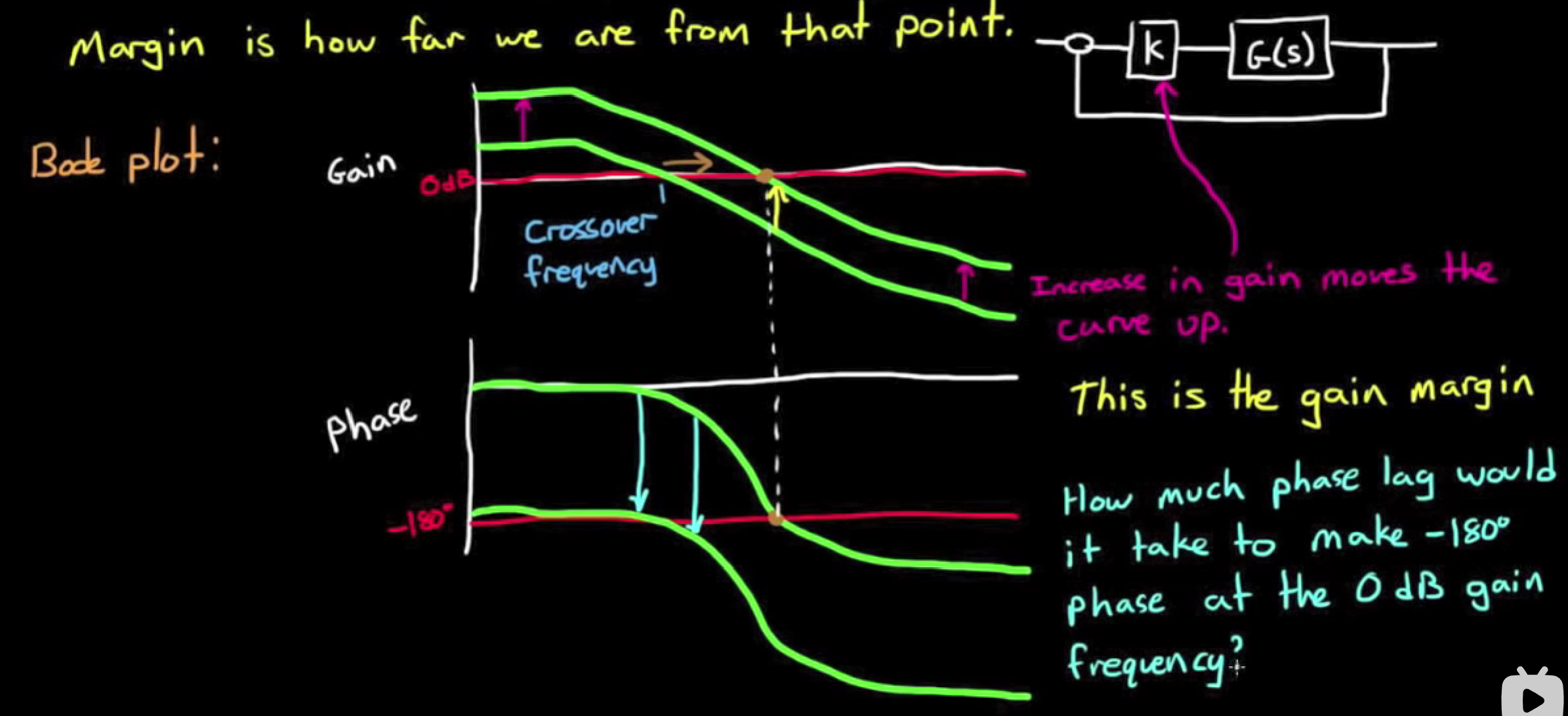
          如图, 相移不变时, 改变增益可能达到这种情况, 导致系统不稳定; 增益不变时, 改变相移也会导致这样的情况.
• 增益裕度是说, 对于一个稳定的系统, 不引入额外相移时, 最多能变化多少dB增益, 使系统变得不稳定;
• 相位裕度是说, 对于一个稳定的系统, 不引入额外增益时, 最多能引入多少相移, 使系统变得不稳定;
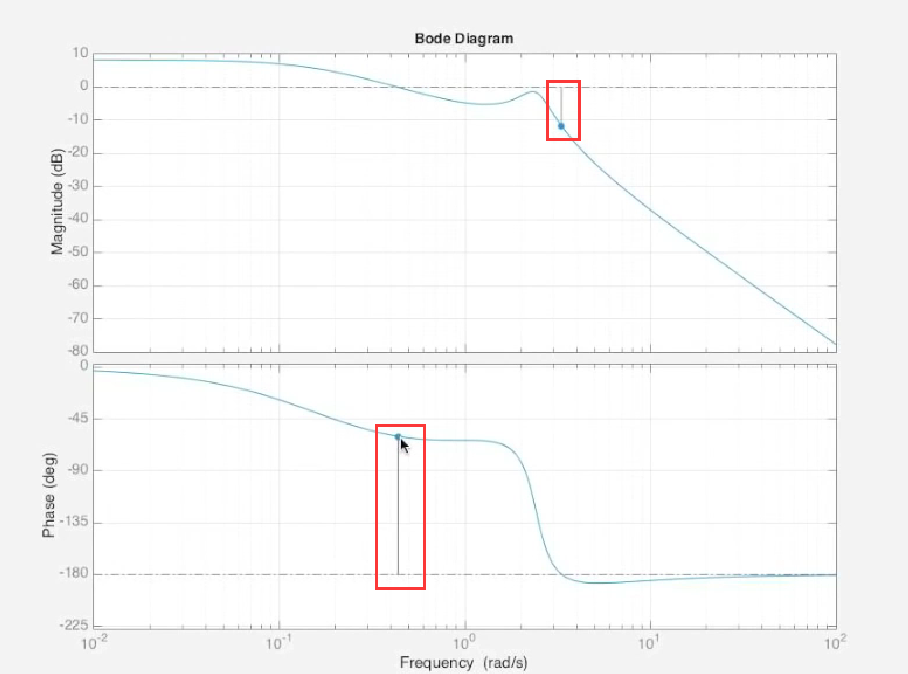
• 在matlab中可以直接从bode plot得到相位裕度和增益裕度
     
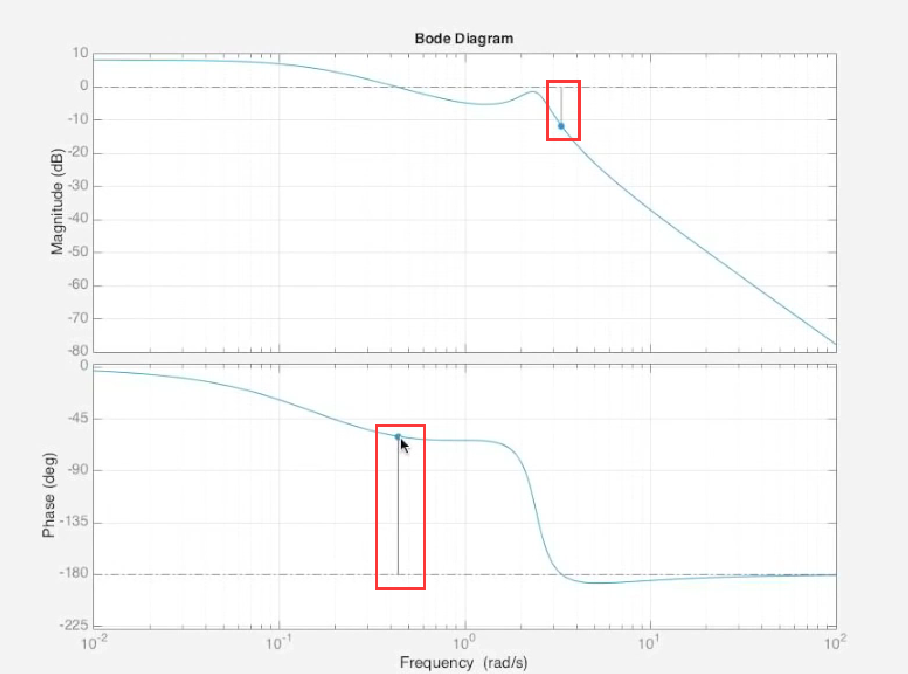
• 一种比较极端的情况如下, 通过bode图可以轻松看出问题所在:
     
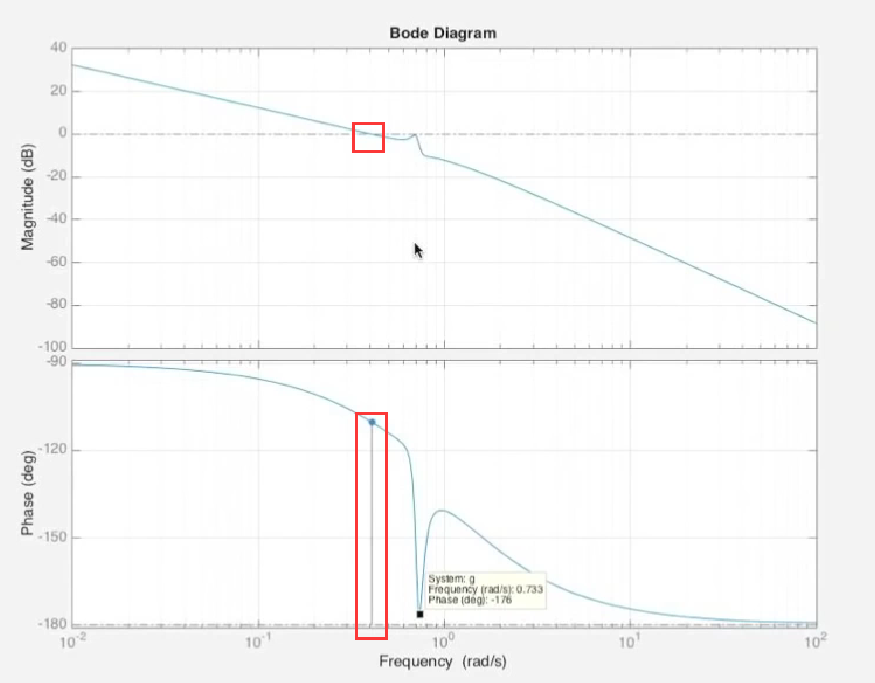
      看上去系统有很高的相位裕度, 因为系统对所有频率都达不到完全的-180°相移, 只能无限逼近, 但是由于有中间的极端的凹陷存在, 实际上只需要引入很小的相移就能造成近似不稳定的情况, 所以这个系统相位裕度并不高.

呜呜呜

• 我写了一大堆用超前滞后滤波器进行补偿, 从而提高稳定裕度的文章, 好像被我弄丢了, 相思了OTZ
• 哈哈哈我找回来了哈哈哈