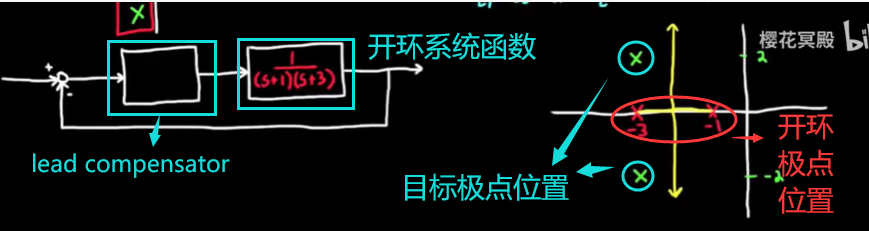
- 假设我们完成了补偿器设计步骤的前两步, 即拥有正确的开环系统函数, 并且选择了超前补偿器, 接下来讲解如何计算超前补偿器的参数, 即如何设计补偿器的零点和极点位置, 使它们对闭环系统极点位置有正确的影响.
补充知识: 主导极点 Dominant Pole
- 有时我们能看到这样的描述: “表现为二阶系统的高阶系统”, 这样的系统能被近似为二阶系统来处理, 是因为有一对主导极点在决定系统的性质.
- 在高阶系统中, 距离虚轴最近的那一对极点是主导极点, 原因如下:
- 如图的二阶系统中, 两个极点分别对应不同的脉冲响应, 但是它们都是指数衰减
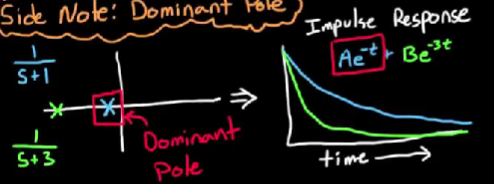
可见, 距离虚轴更远的极点(绿色极点), 脉冲响应衰减很快, 而距离虚轴更近的极点(蓝色极点), 脉冲响应衰减较慢. 将两者叠加起来, 我们能发现蓝色极点主导了脉冲响应的形状, 因为绿色极点对应的响应总是很快就衰减得很小了. 所以我们认为蓝色极点是主导极点. - 如图的高阶系统有很多极点, 但是有一对极点距离虚轴明显比其它极点都近. 结合前文推导, 我们可以想到这对极点对于脉冲响应的形状具有主导作用. 所以他们是主导极点, 并且使系统表现得像二阶系统.

- 如图的二阶系统中, 两个极点分别对应不同的脉冲响应, 但是它们都是指数衰减
补充知识: 为什么我们期待高阶系统表现为二阶系统?
- 我们对系统的性能要求, 例如上升时间, 稳定时间, 通常可以转化为阻尼比和固有频率的代数组合, 而阻尼比+固有频率的组合能使我们方便地确定极点位置, 这样一来, 性能需求到极点位置的转化就很轻松. 例如上升时间
t_r可以计算如下:
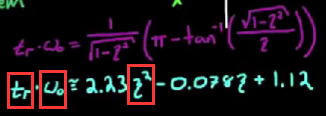
- 问题是上述轻松的转化方法仅限于二阶系统或表现为二阶系统的高阶系统. 所以我们期待高阶系统表现出二阶系统, 否则要得知应该把极点放在哪里不会是一件简单的事情.
使用根轨迹
思路
- 使用根轨迹来设计超前补偿器, 最直观的思路是将闭环增益作为变化的参量, 设计超前滤波器的零点和极点位置, 使根轨迹穿过系统需求对应的极点位置, 最后算出使极点移动到正确位置的增益, 即完成了补偿器的设计.
实例
举例如下, 我们有一个开环系统, 打算为它设计一个超前补偿器
黄色轨迹是根轨迹, 可见对系统进行单纯的闭环控制并不能使极点移动到目标位置处, 换句话说, 根轨迹不穿过那个位置. 接下来, 通过引入超前补偿器, 我们能将跟根轨迹扭曲一下, 让它穿过目标点.
- 一个在开环根轨迹上的点α, 具有以下规律: 有点类似与Nyquist plot那一套, α与极点连线的夹角之和, 减去α与零点连线的夹角之和, 等于180°
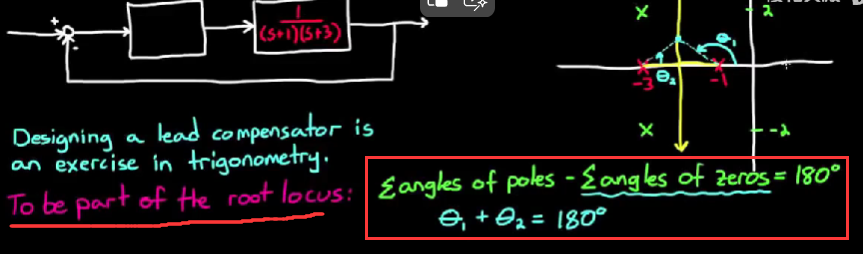
用这个规律, 我们可以先将超前补偿器的零点放在一个合理的位置, 然后通过角度的计算得到超前滤波器极点的位置. - 如何找到超前补偿器零点的放置位置? 它可不能随便放, 举两个极端的例子:
- 我们把零点放到无穷远处, 然后观察那个判断某一点α是否在根轨迹上的角度公式, 我们能发现在上面具体的例子中, 目标极点位置α与两个开环极点连线的夹角之和为225°. 由于零点与α夹角近似为0, 减去这个角度, 夹角之和仍然为225°, 而我们还有一个补偿器的极点没有放置, 也就是说最终夹角之和必定大于等于225°, 这意味着α不可能在根轨迹上. 只有零点的位置产生了足够的夹角, 减去这个夹角, 使夹角之和能够小于180°, 才能使α有在根轨迹上的可能性.
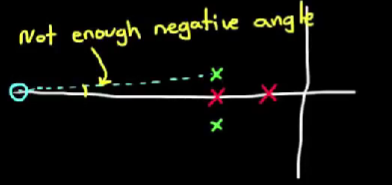
- 我们把零点放在很偏右的位置, 此时零点产生的夹角确实足够了, 但是最终计算出的补偿器的极点的位置可能比原来的开环极点还要靠近虚轴, 这样会改变系统的主导极点, 破坏系统是二阶系统这一属性. 介于我们已经讨论过二阶系统的重要性, 这种做法是得不偿失的.
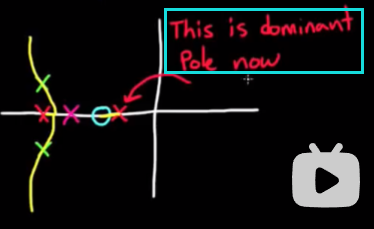
- 所以零点的摆放位置应该介于两者之间.
- 我们把零点放到无穷远处, 然后观察那个判断某一点α是否在根轨迹上的角度公式, 我们能发现在上面具体的例子中, 目标极点位置α与两个开环极点连线的夹角之和为225°. 由于零点与α夹角近似为0, 减去这个角度, 夹角之和仍然为225°, 而我们还有一个补偿器的极点没有放置, 也就是说最终夹角之和必定大于等于225°, 这意味着α不可能在根轨迹上. 只有零点的位置产生了足够的夹角, 减去这个夹角, 使夹角之和能够小于180°, 才能使α有在根轨迹上的可能性.
- 针对这个例子, 正确解法如下:
- 选择合适的零点位置, 例如(-4, 0j)

- 根据零点位置得到角度信息, 根据角度信息计算极点位置
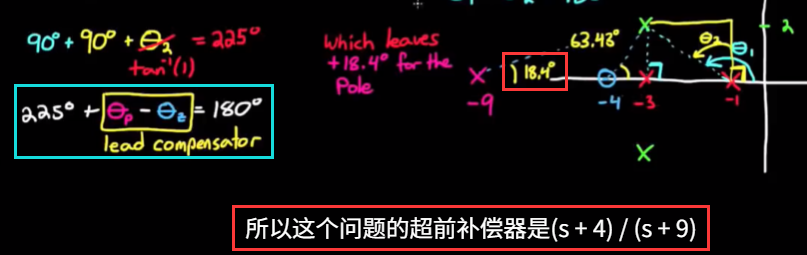
- 用一些方法计算出闭环增益, 例如使用matlab
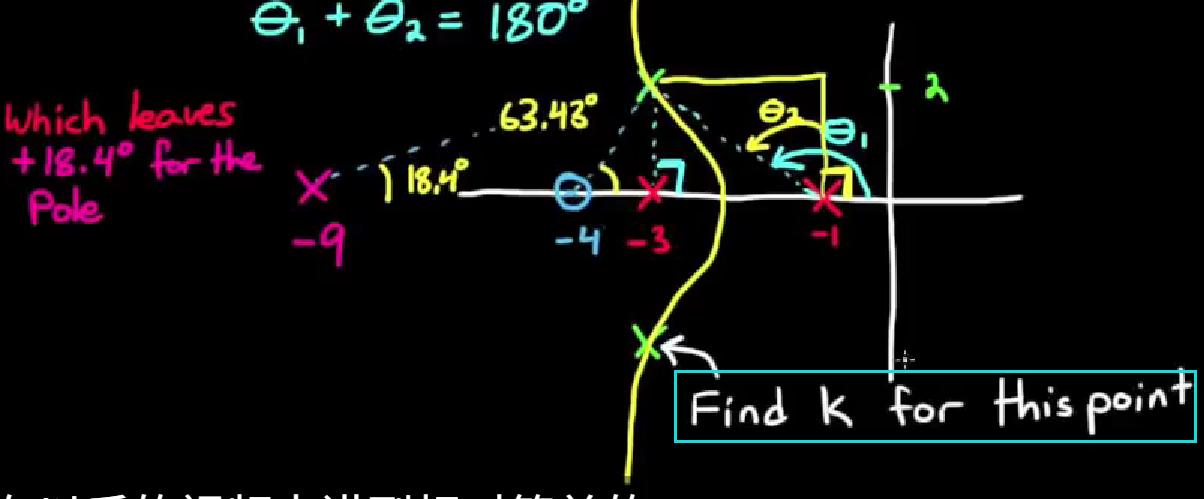
- 选择合适的零点位置, 例如(-4, 0j)
补充知识: 超前补偿器的特点
- 给开环系统设计闭环的超前补偿器后, 系统仍然有不稳定的可能性, 因为在一些高阶系统中, 加入超前补偿器可能会使一些本来稳定的极点移动到右半区.
- 一般来说, 我们应该先尝试PID控制器, 因为它更直观, 当PID不能完成任务时再考虑超前补偿器
- 使用超前补偿器的系统响应相比PID更快, 但是无法消除稳态误差, 而且会放大高频噪声.
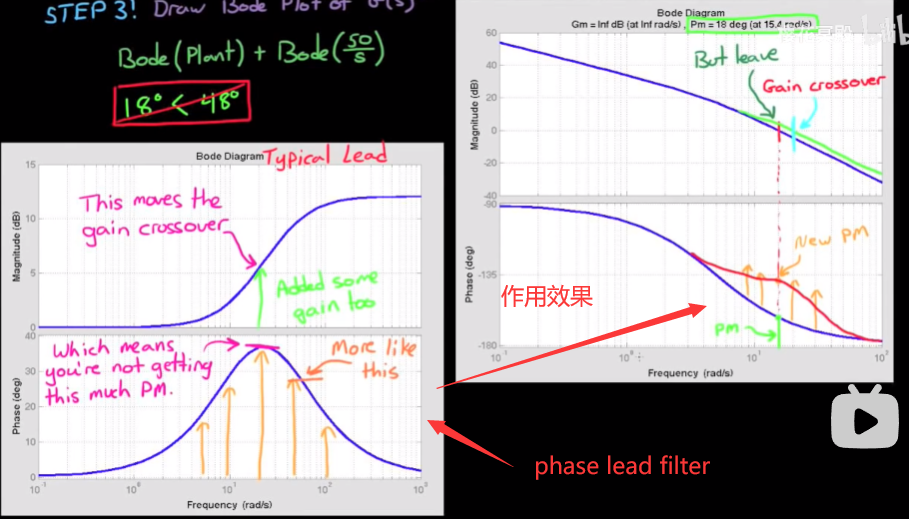
使用bode plot来设计
思路
- 使用root locus根轨迹来设计超前补偿器, 需要我们先将性能需求转换为极点位置, 而使用bode plot来设计, 需要我们将性能需求转换到频域上, 频域上的指标有相位裕度, 增益裕度, 带宽, 截止频率, 零频率幅值, 稳态误差(利用终值定理求得), 如下图
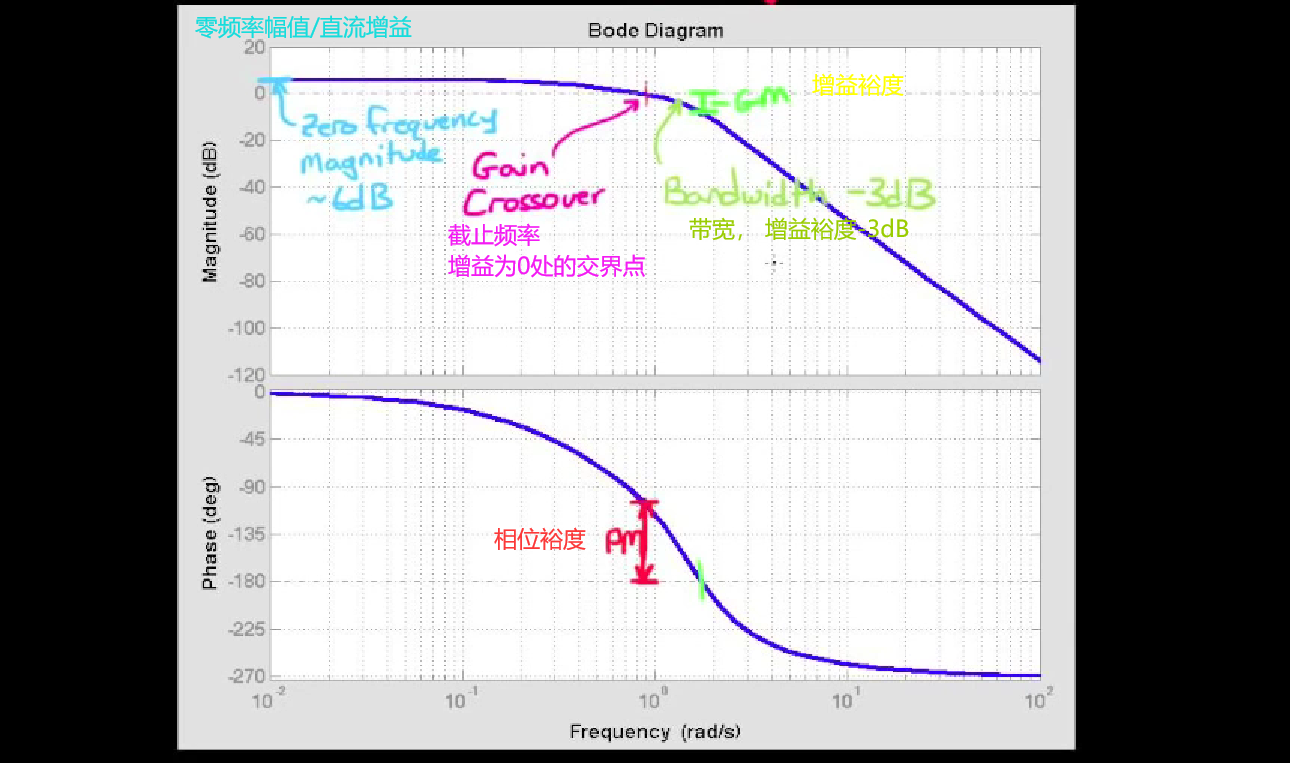
图片有错, 带宽是增益为-3dB时的频率, 重新截图太麻烦懒得搞了:-p - 一旦能把需求转移为频域的指标, 接下来只要操纵bode plot的形状, 即可满足需求
实例
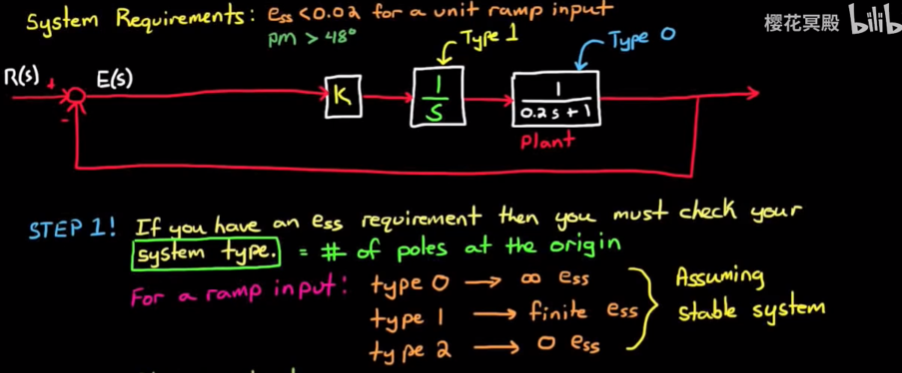
设系统需求为单位斜坡响应的稳态误差
e_ss< 0.02, 相位裕度pm> 48°, 开环系统函数为 1 / (0.2s + 1).
- 有稳态误差和相位裕度两个需求, 我们一般先解决稳态误差, 因为稳态误差的约束可能需要加入积分器, 如果先设计了相位裕度, 积分器会对相位产生影响, 那就白设计了.
- 这里需要特别对稳态误差的计算做复习. 本人学习的时候搞半天没理解为什么2型系统能够0误差追踪斜坡输入, 我之前做笔记的时候也没有认真学习和记录这一点, 所以几乎没有印象, 下附关键公式:
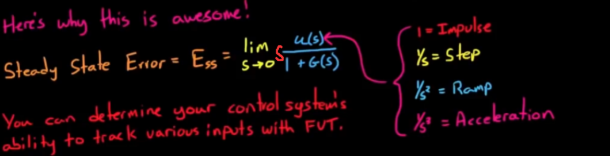
根据题目
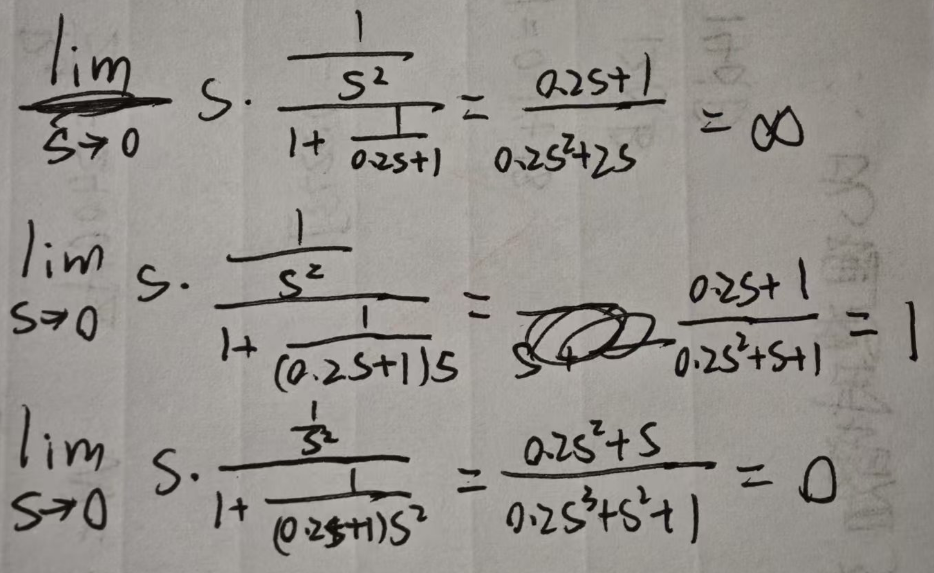
从上到下分别是 原系统/原点加1个极点/原点加2个极点 的稳态误差, 由此可见开环系统确实无法跟踪阶跃信号. 我们要满足稳态误差的需求, 首先要让系统从type 0变为type 1以上的系统. - 然而系统类型并不是越高越好, 原点处加入极点, 在现实意义上的是有开销的, 这里给出稳态误差的要求并不为0, 所以我们把它设计成有误差的就行, 没必要追求0误差. 于是我们向系统加入一个积分器, 使其从type 0变为type 1.
- 根据
e_ss< 0.02, 注意到闭环增益k直接影响e_ss大小, 带入闭环增益k计算稳态误差, 考虑k的取值范围如下:
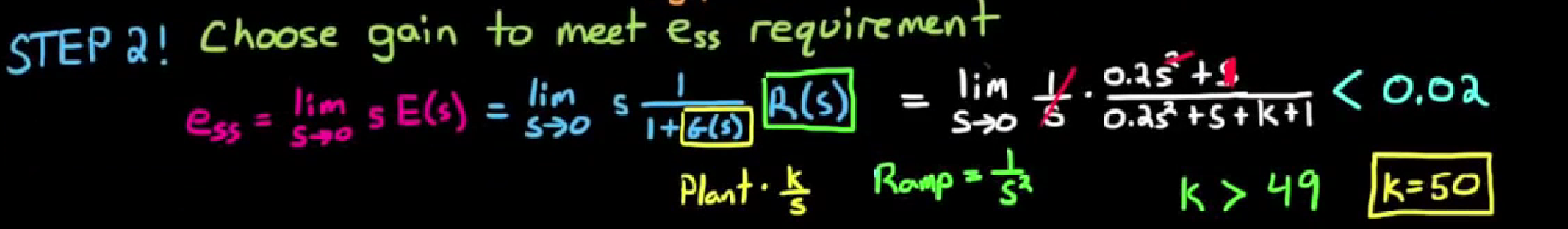
为了计算方便, 取k = 50. - 我们已经满足了稳态误差的需求, 接下来将系统组合起来画出bode plot, 分析相位裕度
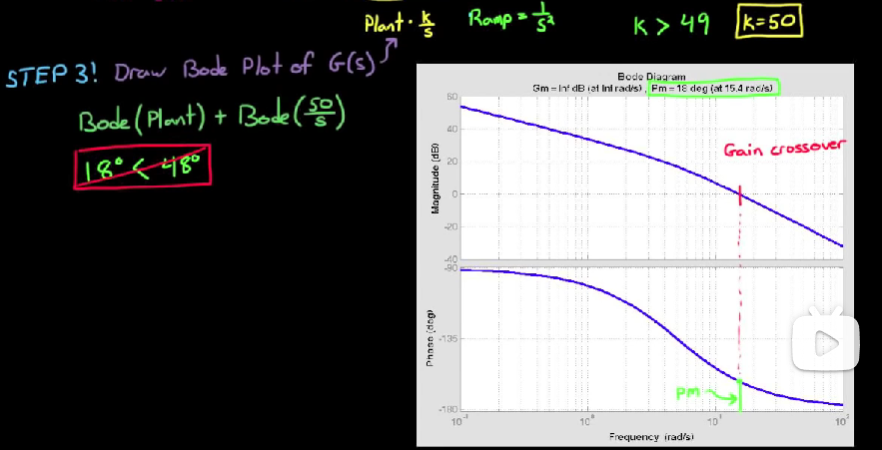
可见相位裕度为18°, 不满足需求, 接下来该超前滤波器出手了. - 画出超前滤波器的bode plot, 可以看到它只对特定频域的相位超前, 如果我们能将这个频率设定在转折频率附近, 那就能起到在衡量相位裕度的频率附近增加相位, 而不影响其它频率的效果
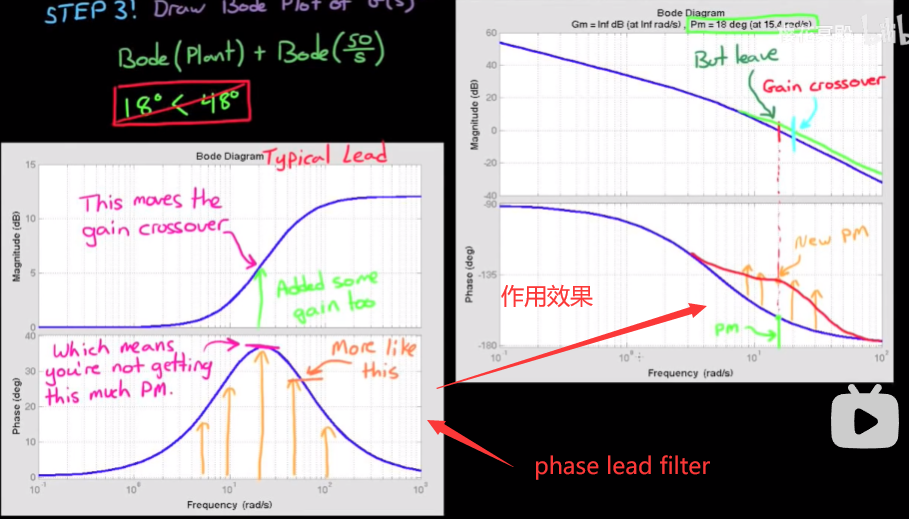
值得注意的是, 它会在转折频率附近增加增益, 导致转折频率略微右移. - 要设计合适的超前滤波器, 就需要知道滤波器的数学表达式中, 包含了哪些关于滤波器形状的信息. 相位超前滤波器可以写成这个形式:

为什么写成这样? 因为可以根据这些参数了解到滤波器的形状:
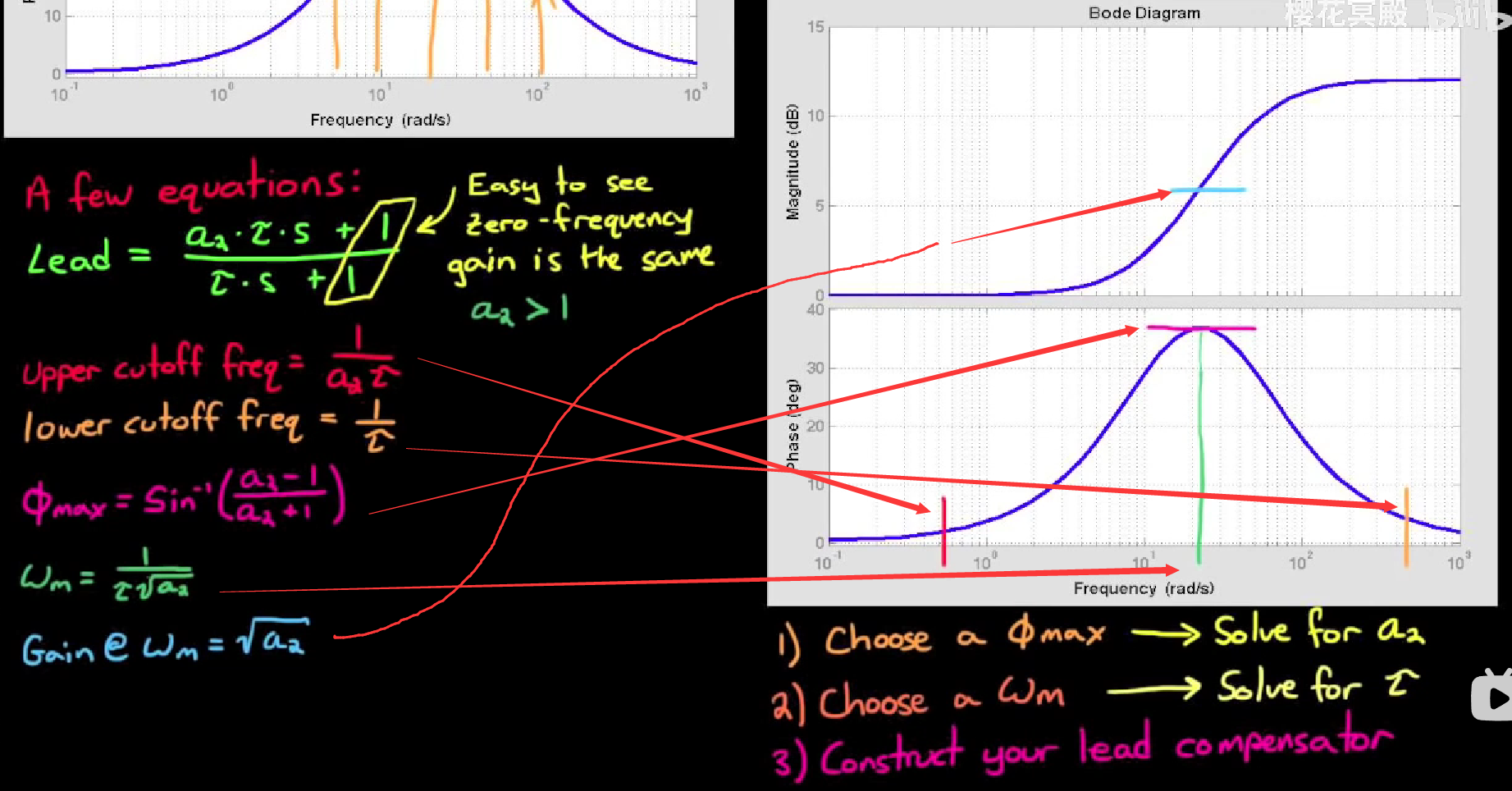
比较关键形状参数的就是相位超前滤波器作用的中心频率, 超前的相位, 以及这个频率下增加的增益. 设计步骤在图片右下角, 很清晰了. - 设计滤波器时, 滤波器超前的最大相位不能仅仅设计得刚好满足需求, 因为引用滤波器会带来额外的增益, 导致实际转折频率右移. 设计的相位超前刚好够用, 实际应用上以后转折频率偏移, 实际相位裕度又不够用了. 所以设计最大相位的时候要留一些余量, 或者用一系列参数反复尝试直到频率偏移后, 相位裕度仍然够用.
- 最终设计的超前补偿器如下:
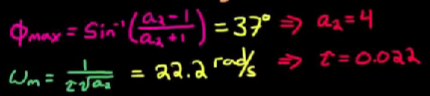
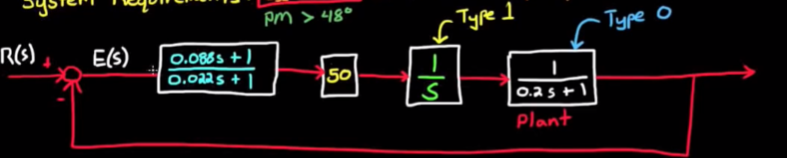
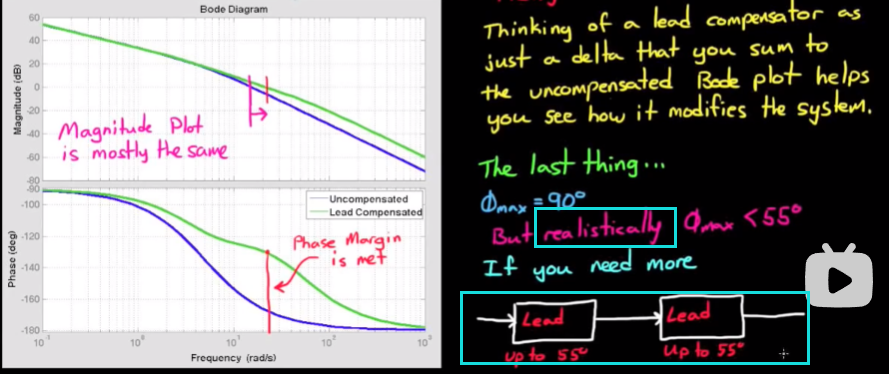
可见相位在我们需要的地方有一个滑稽的突起, 满足了我们的所有需求.
Brian在最后也提到, 虽然理论上相位超前滤波器能提供最大90°的超前, 但是从实际设计来看, 最大超前约为55°, 否则硬件设计将会变得不实用. 如果想要55°以上的超前, 级联两个滤波器即可.