夏远的个人主页——滞后补偿器设计

仍然假设我们拥有正确的开环系统函数, 并且选择了滞后补偿器, 接下来讲解如何放置补偿器的零点和极点.
首先要知道我们为什么选择滞后补偿器, 前文中提到超前补偿器能够重塑根轨迹, 增加相位裕度, 滞后滤波器与超前滤波器的作用并不是对偶的关系, 它的主要用途是减小稳态误差, 而且尽量不影响根轨迹.

使用根轨迹

思路

与设计超前补偿器时类似, 我们有一对零极点要放置, 优先放置零点, 然后根据一些规则确定极点的位置, 即可完成滞后补偿器的设计.

补充知识: 滞后补偿器如何减小稳态误差?

从数学的角度考虑, 画出开环系统 G(s) = G_n(s)/G_d(s) 的闭环控制框图, 我们可以计算出加入滞后补偿器滞后的阶跃输入稳态误差, 如图

最终我们可以将需求的稳态误差带入最下面的等式中, 得出零点与极点的位置关系. 反过来说, 通过设计零点和极点的位置, 我们能够控制稳态误差, 以上就是从数学上进行的证明.
然而值得注意的是, 要想使稳态误差 = 0, z/p -> ∞, 这在现实世界中不可能实现, 所以一般我们只说减小误差, 而不说消除误差.
从实际作用效果的角度来看, 稳态误差基于系统在低频段的特性, 即s->0时的特性, 那么对比滞后补偿器和超前补偿器:
- 超前补偿器主要是提高高频增益, 从而改善动态响应(例如提升相位裕度), 但是对稳态误差无帮助;
- 滞后补偿器则是提升低频增益, 即除了闭环增益k之外, 还有额外的增益, 鉴于稳态误差的计算规律如下:
  
  可以看到整体增益越大, 稳态误差越小, 所以滞后补偿器具有减小稳态误差的功能.

实例

我们继续对已经设计完成的有超前补偿器的系统进一步设计, 对以下系统, 有稳态误差 = 0.1的需求, 设计一个滞后补偿器

首先求零极点位置比例:
在哪里放置我们的零点呢? 回忆我们在使用根轨迹设计超前滤波器的时候提到的规律, 一个点α在根轨迹上的条件是:
- 为了尽量不影响根轨迹, 我们需要保证零点和极点与根轨迹上任一一个点的夹角要近似相等. 这样就引出两种可能性, 这对零极点在很偏左的位置或者很偏右的位置.
- 然而将零极点放置在左边的方案, 除非放在无穷远处, 否则位置的比例关系会使得夹角难以相等; 放在右边的方案, 随着极点靠近虚轴, 零点也会很靠近极点, 导致夹角值越来越逼近, 如下图所示:
  
  所以将零点放在距离虚轴很近的地方, 极点紧凑地放在旁边, 是最好的方案. 当然零点也不能离虚轴太近, 因为这样会导致硬件设计成本提高. 按照经验来说, 将零点放在主导极点实坐标的1/50处会比较好.
根据1/50这个经验, 我们可以找到零点和极点的位置
最后应用我们计算出来的滞后补偿器

在matlab中画出阶跃响应, 可以看到稳态误差明显减小, 保持在0.1左右. 并且脉冲响应没有显著的变化, 因为我们斌没有改变主导极点对系统的影响.

问题: 为什么我把一个极点放在离虚轴很近的地方, 没有改变系统的主导极点?

原因之一：偶极子效益
当补偿器的零点和极点非常接近时（即两者在复平面上的距离远小于它们到原点的距离），它们的动态效应会相互抵消
原因之二：

主导极点主要决定的是系统的瞬态响应，滞后滤波器影响的是稳态响应，所以即使从位置上看，之后滤波器的极点改变了主导极点，但是实际上并没有太大的影响

使用bode plot

思路

用bode plot设计超前滤波器时，我们的思路是尽量影响增益，只影响转折频率附近的相位, 从而增加相位裕度.
而使用bode plot设计滞后滤波器时, 因为滞后滤波器只能带来相位滞后即减小, 如果作用在转折频率处, 相位裕度会进一步减小. 我们的思路是通过影响增益从而移动转折频率, 并且让滤波器对相位的影响区域尽量避开移动后的转折频率, 从而提高相位裕度.

实例

老朋友

第一步还是满足稳态误差的需求, 和设计超前补偿器时的例子一样, 首先在原点处加一个极点, 是系统变为type 1, 这样就能追踪斜坡响应, 然后设计合适的增益使稳态误差降低到一定的值. 这个过程之前已经说过, 在此略过
第二步是画出bode plot观察, 看看我们可以如何移动转折频率

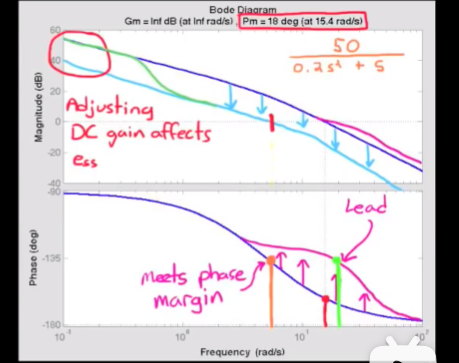
如图, 同时画出了超前补偿器和滞后补偿器增加相位裕度的方法. 我们需要利用滞后补偿器将一定频率范围以后的增益都降低, 起到移动转折频率的的效果. 同时注意不能改变低频部分, 也就是频率接近0的部分, 因为直流增益影响到稳态误差, 如果改变直流增益会使满足稳态误差要求的系统设计失效.
我们先来认识一下滞后补偿器的bode plot, 以下是一个例子:

有几个关键点:
1. 可以看到图片右侧的公式中有两种滞后补偿器的写法, 上方的写法是正确的, 因为它保证s->0时增益为1, 而下方的写法虽然直观地表现了零极点的位置, 直流增益却不等于0.
2. 看bode plot增益图的整体, s->0, gain = 0dB, s->∞, gain = -6dB, 对高频有衰减的增益; 看相位图的整体, 在s->0, s->∞时, 相位滞后几乎为0, 在频率的中间区域有一段相位滞后.
3. 基于这个特性, 我们可以利用高频的增益衰减来移动转折频率, 而几乎不改变相位; 相位滞后的区域尽量远离转折频率放在低频区域, 这是可以接受的.
第三步是计算补偿器的增益衰减量, 先假设相位没有任何变化, 在图上找出相位裕度大于48°的点, 再找到对应增益图中的点位, 比较一下就知道理论上要多少增益衰减.

但是由于实际上相位会有一定滞后, 也就是说按照理想方案设计, 最后相位裕度会刚好不够一点, 所以在设计补偿器的时候留一些余量, 例如理想方案增益为-18dB, 实际设计-20dB的增益.
第四步是计算零极点的位置. 首先根据目标增益-20dB, 得到实际增益是1/10, 1dB = 20log(输出/输入). 也就是说滞后补偿器按照以下表示方法:

s的系数会有10倍的关系, 也就是零点的实坐标是极点的实坐标的10倍.
接下来摆放零点. 由于现实因素限制, 还是将零点放在主导极点实坐标的1/50处, 然后放置极点, 就完成了滞后补偿器的设计.
在matlab中画出原闭环系统, 加入超前补偿器的系统, 加入滞后补偿器的系统三个bode plot并合并, 看看效果

闭环系统阶跃响应如图